这章分为三部分:
Part1:调和级数
Part2:阶乘
Part3:调和级数、阶乘与三角函数之间的联系
Part1
第一节:调和级数的引入
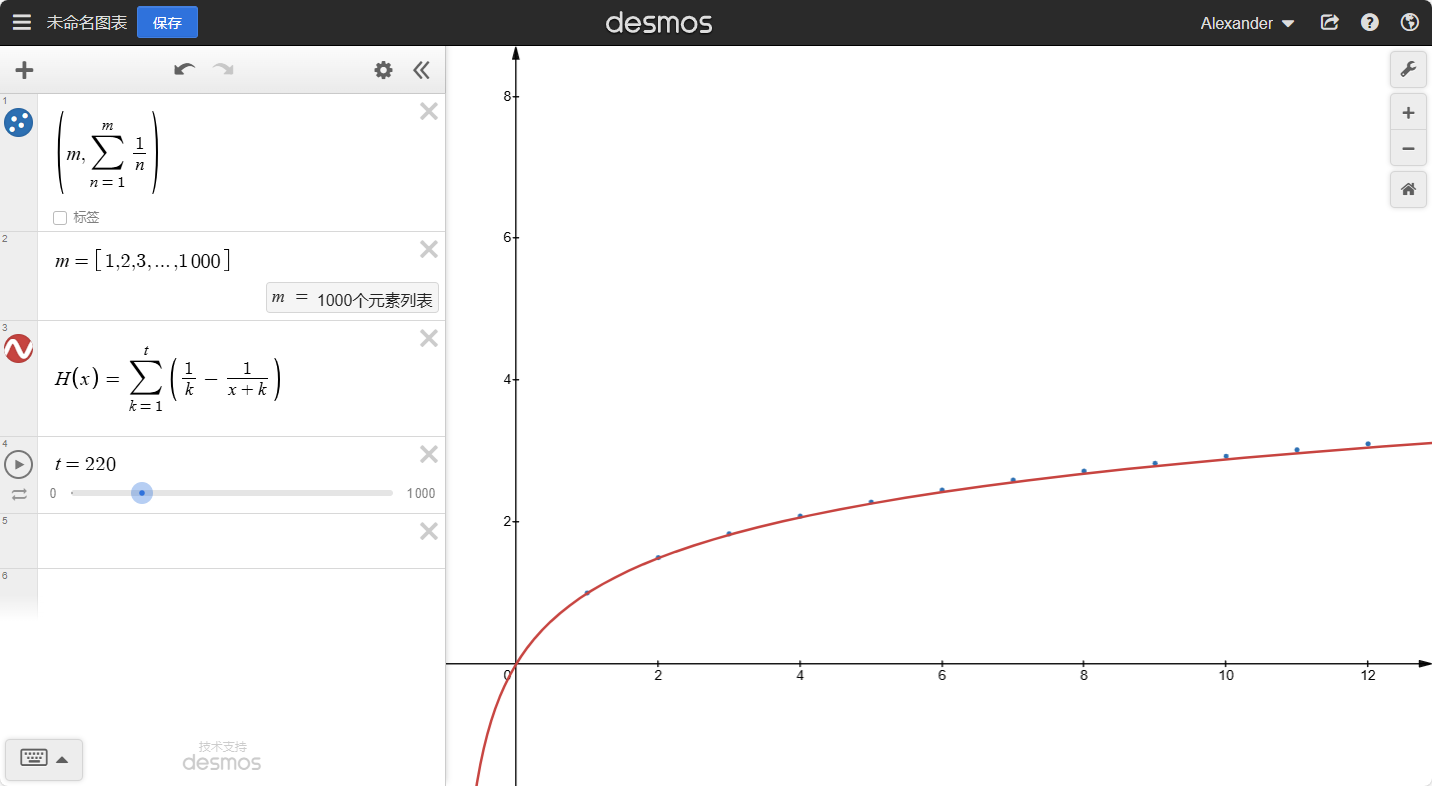
什么是调和级数呢?我们定义:调和级数H(x)满足:
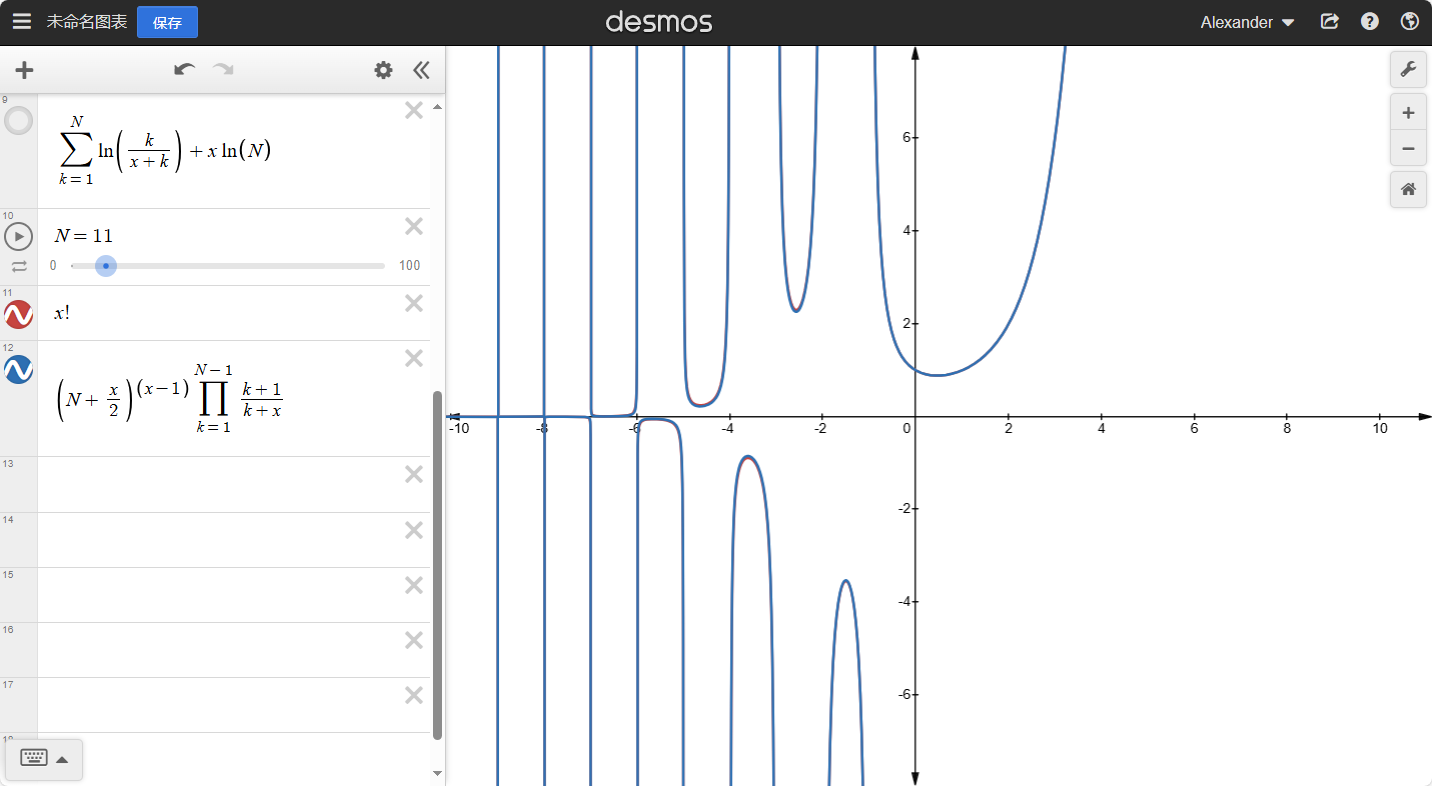
H(x)=k=1∑xk1
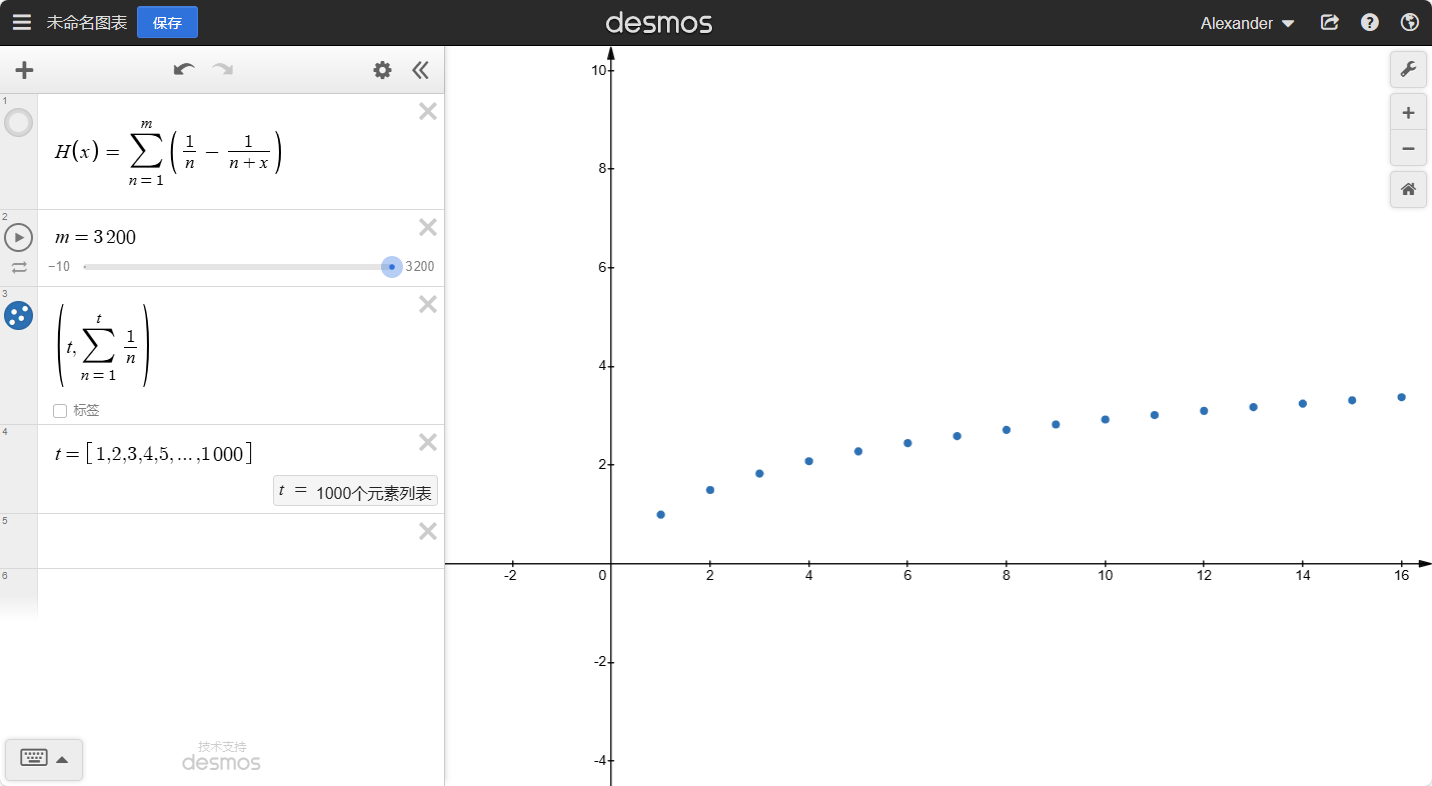
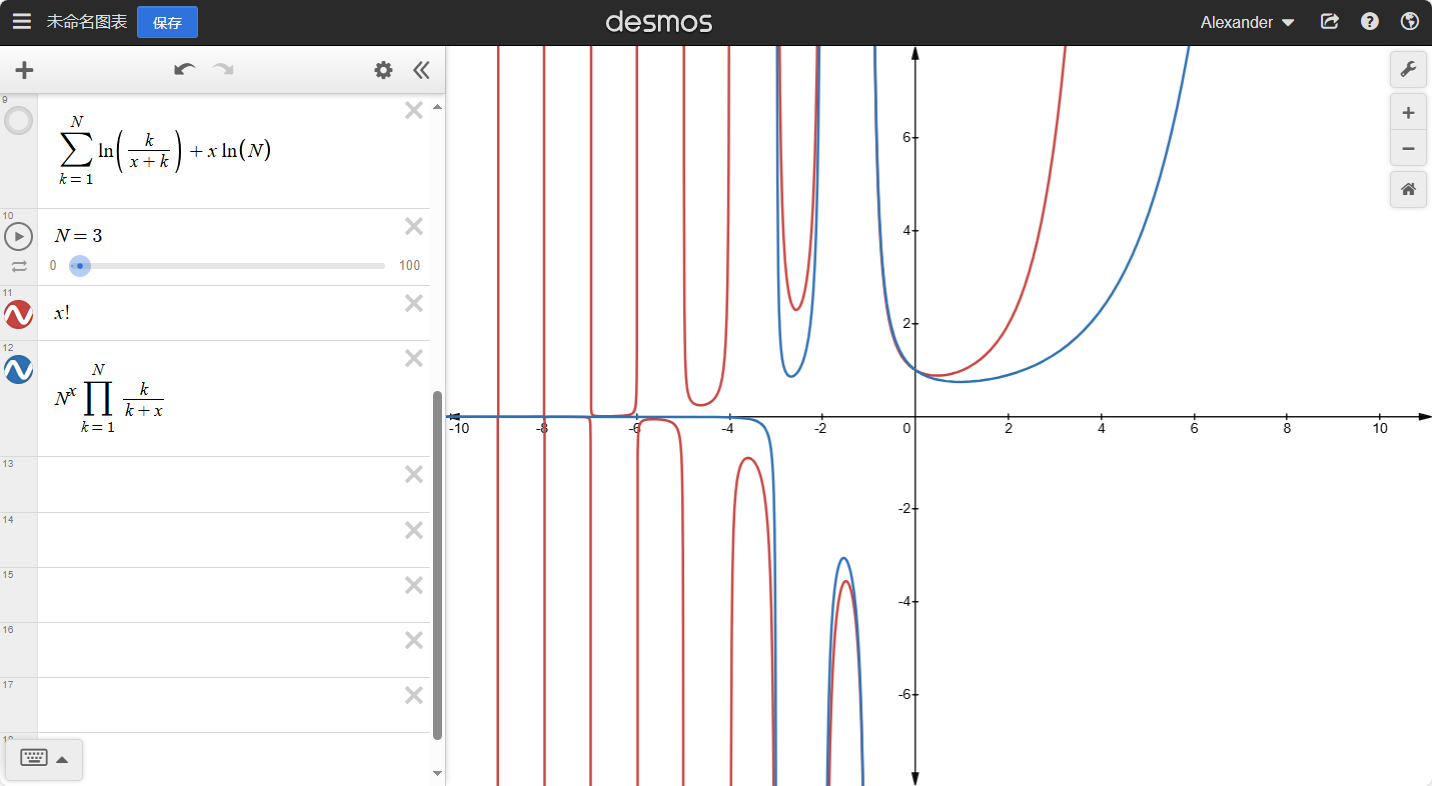
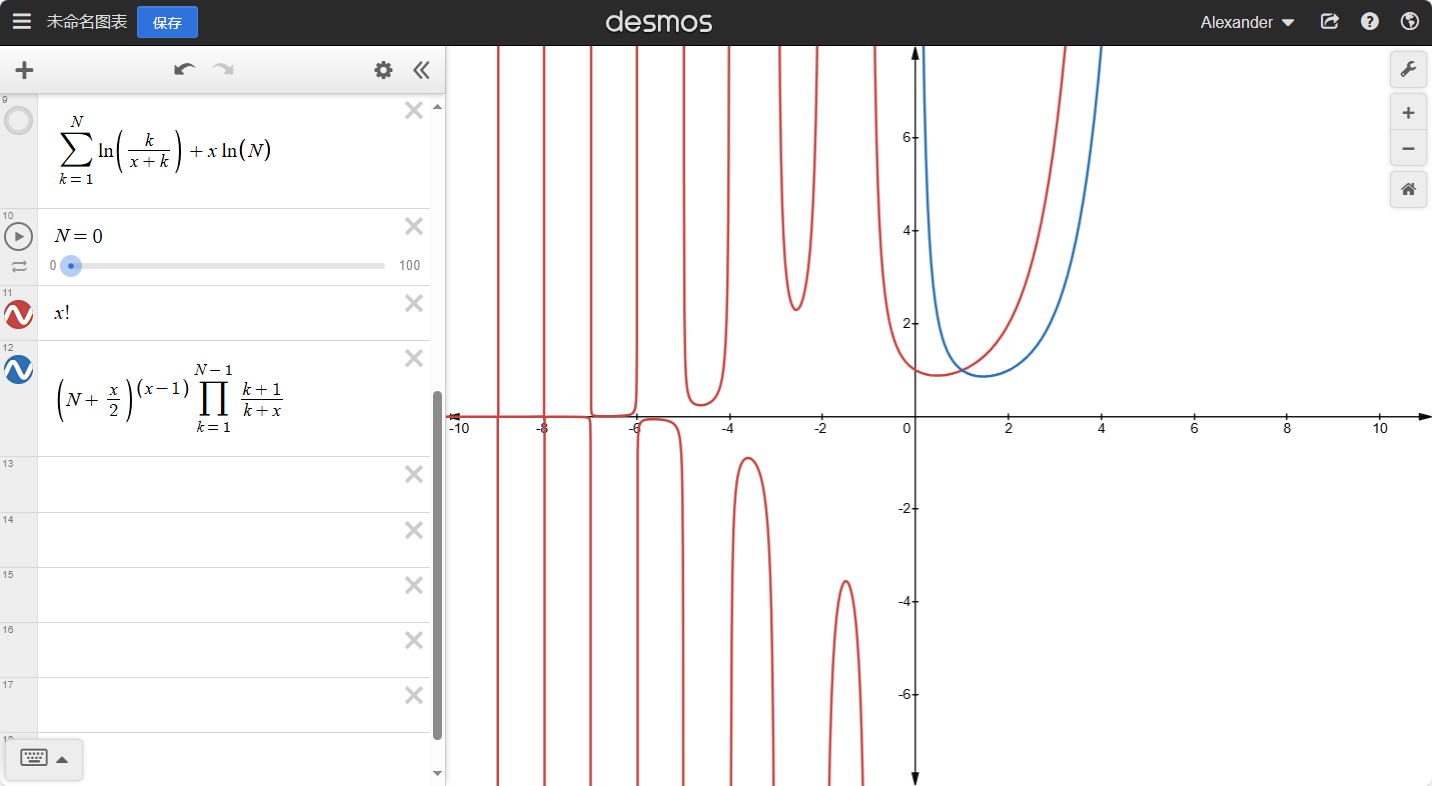
这个散点函数的图像长什么样呢?

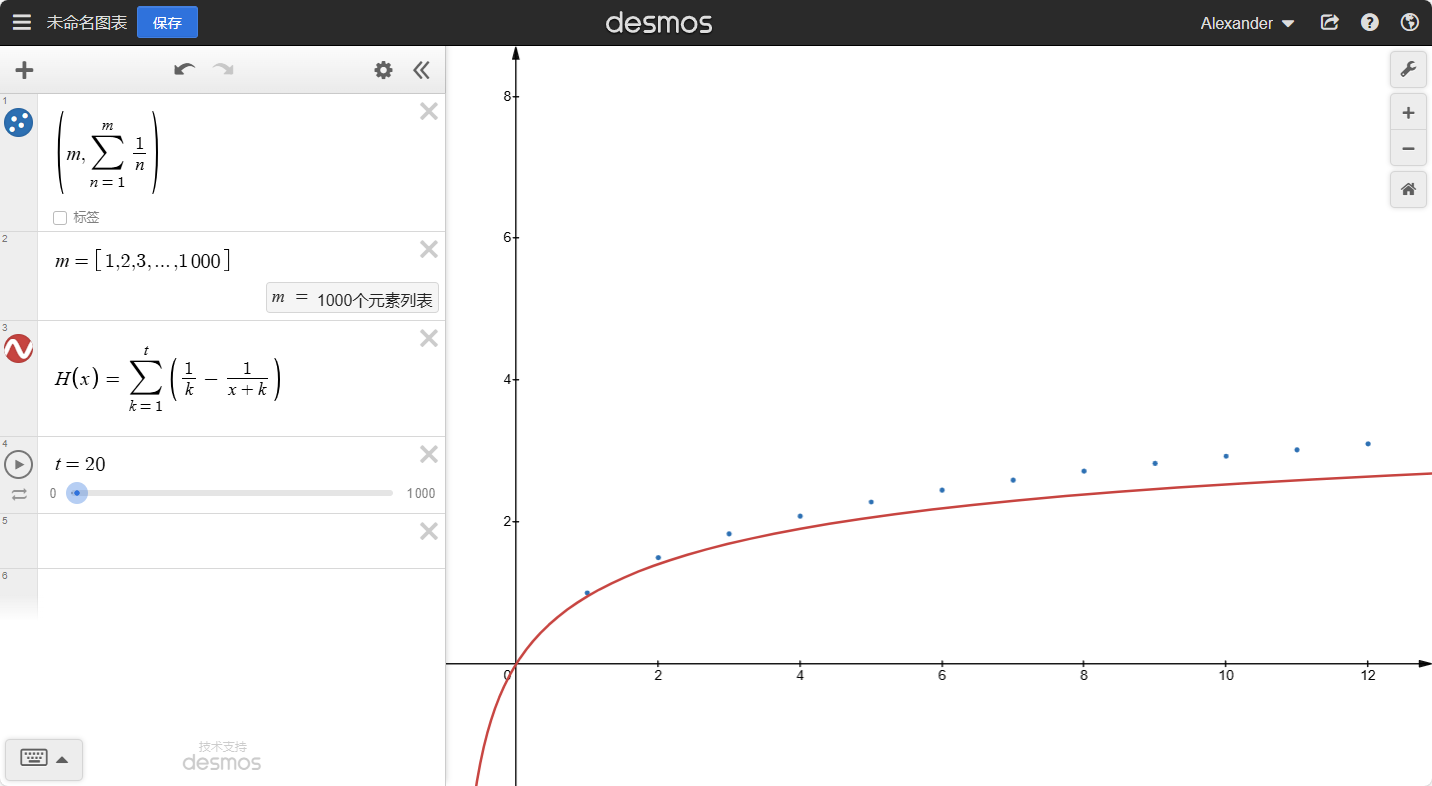
红线与蓝线在x∈[0,+∞)上的交点是我们想象的散点,但是事实上,我们可以将H(x)扩充到实数。
H(x)=k=1∑∞(k1−k+x1)
第二节:扩充调和级数

首先,我们可以轻松得到以下两个式子:
H(x)=H(x−1)+x1H(x+n)=H(x)+k=1∑nx+k1
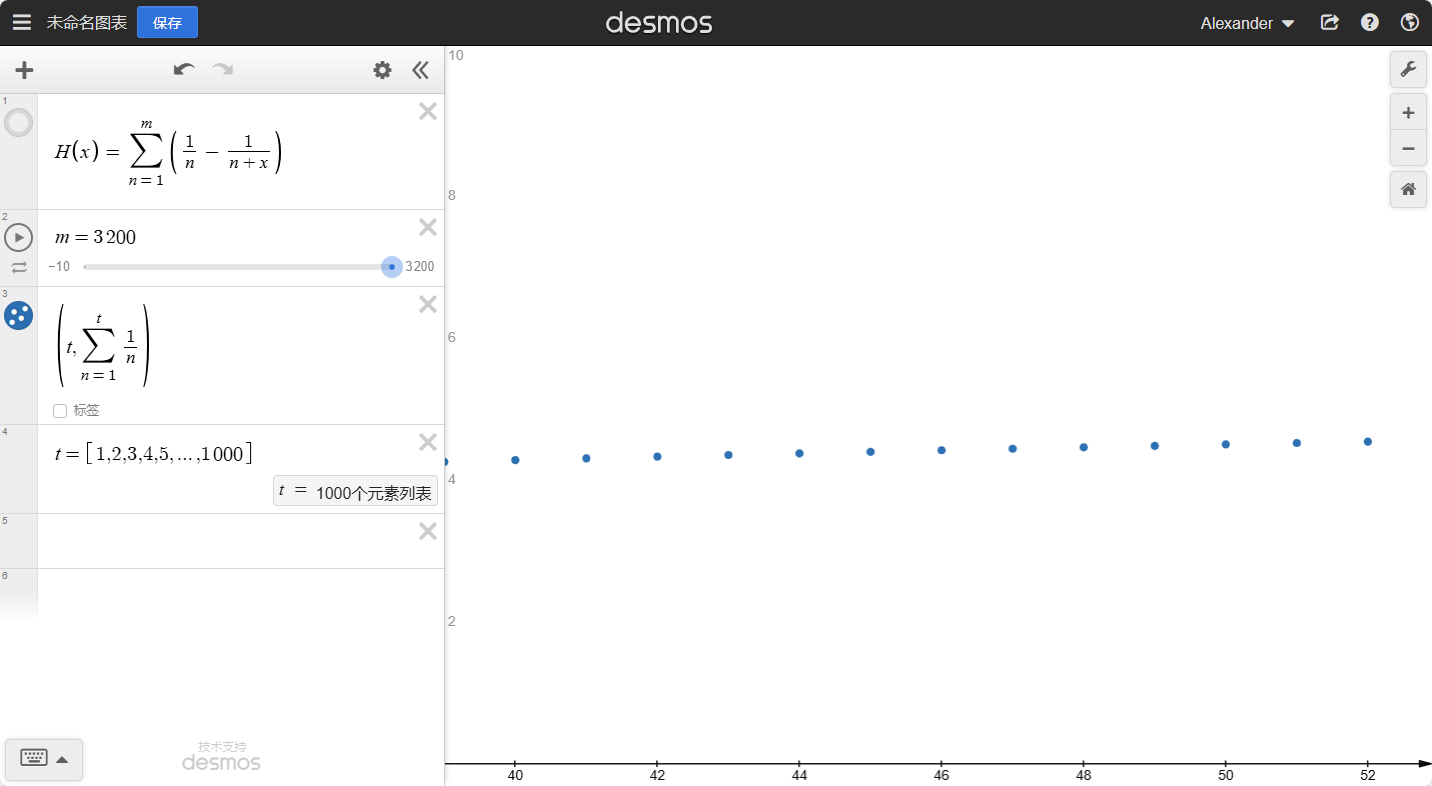
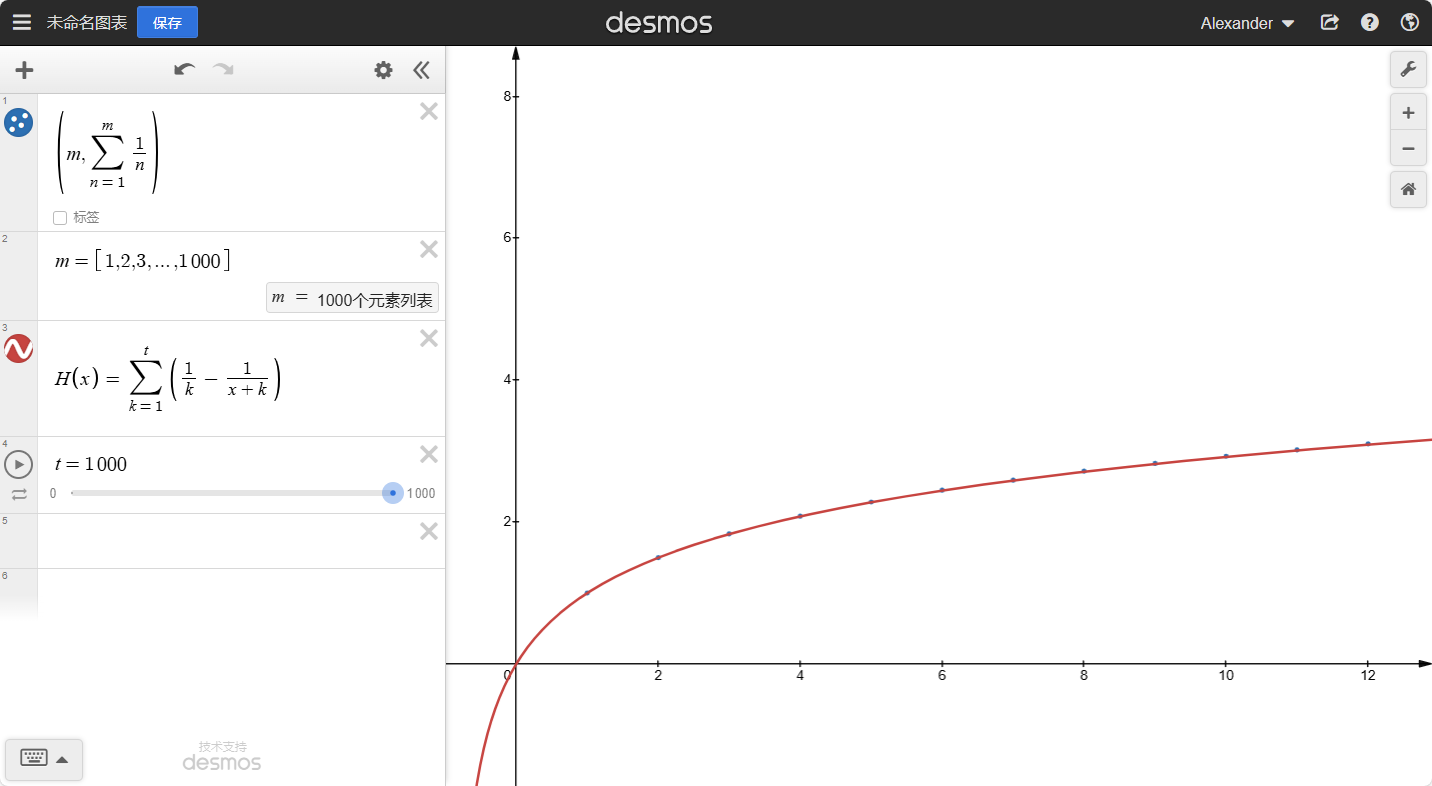
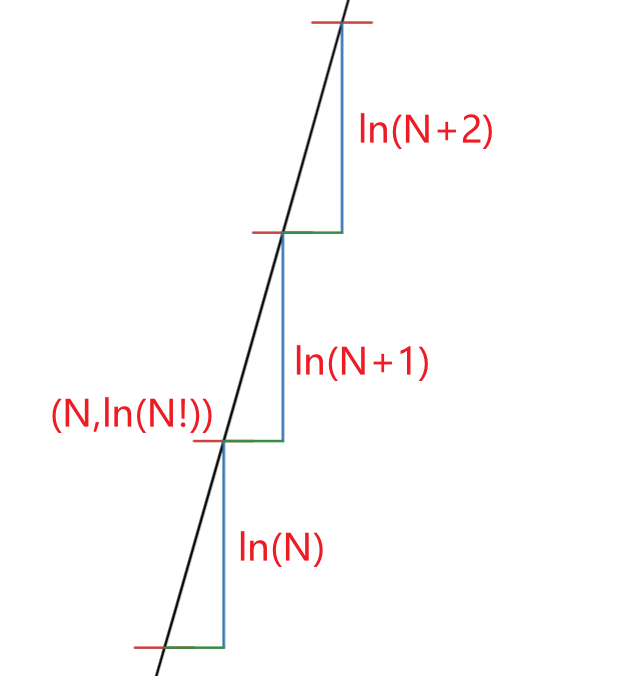
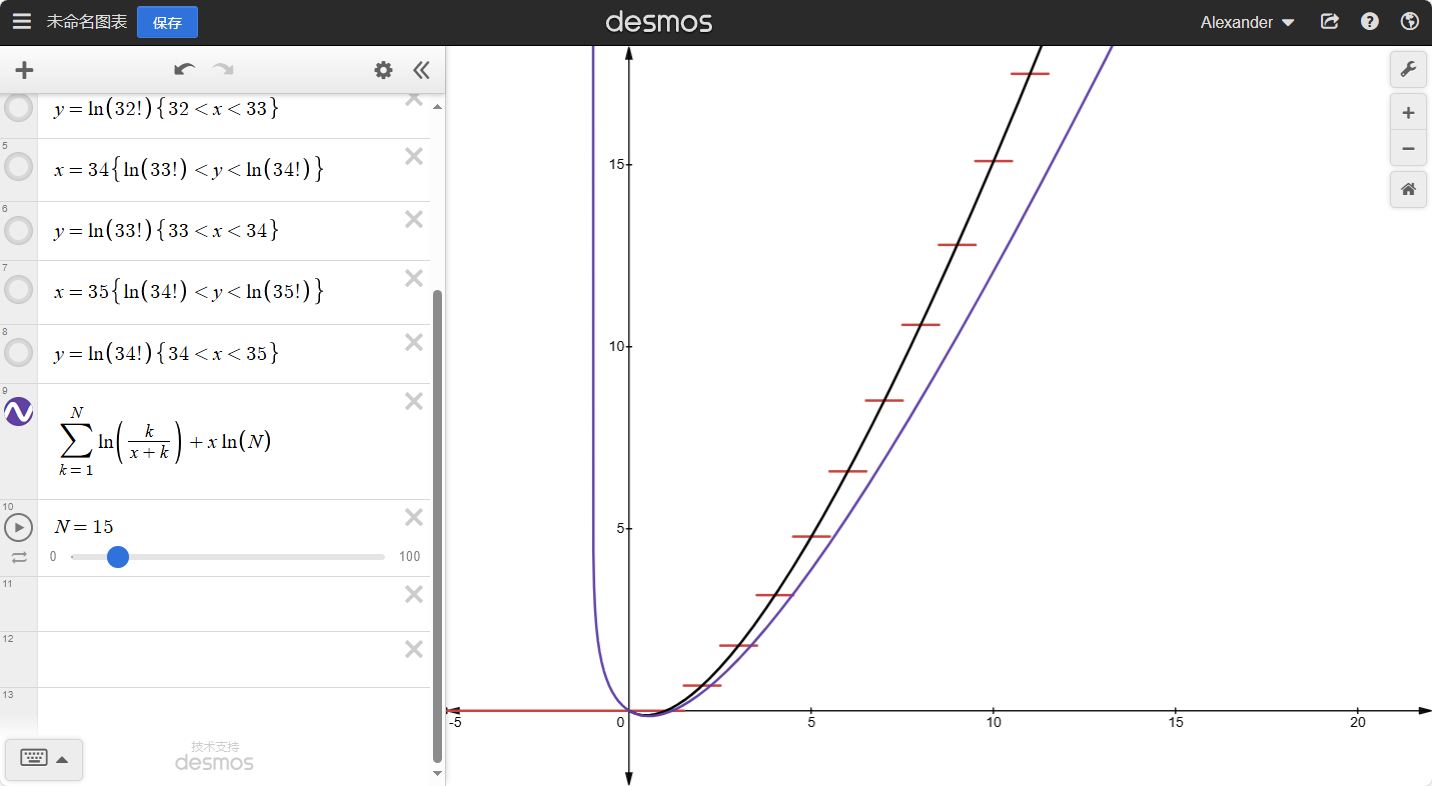
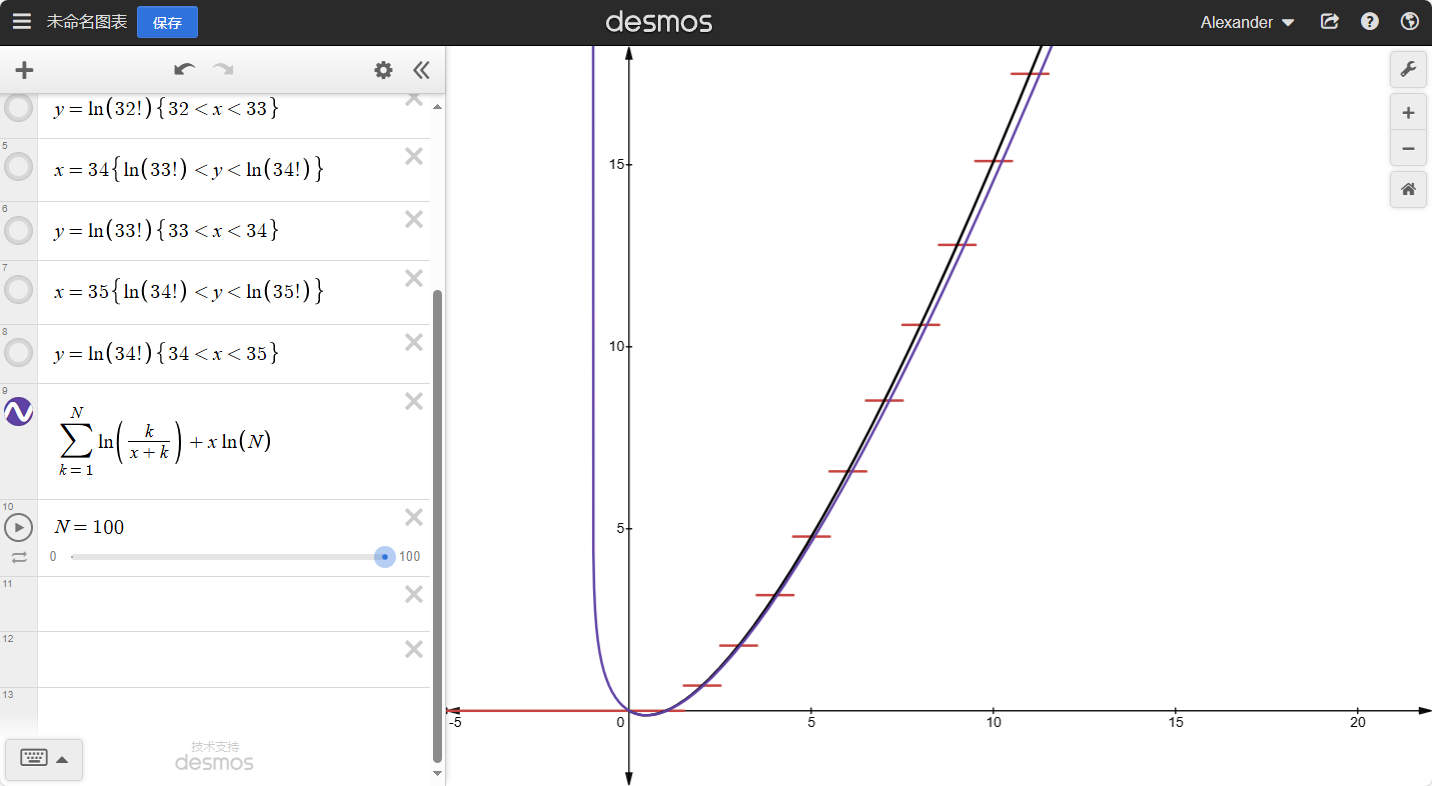
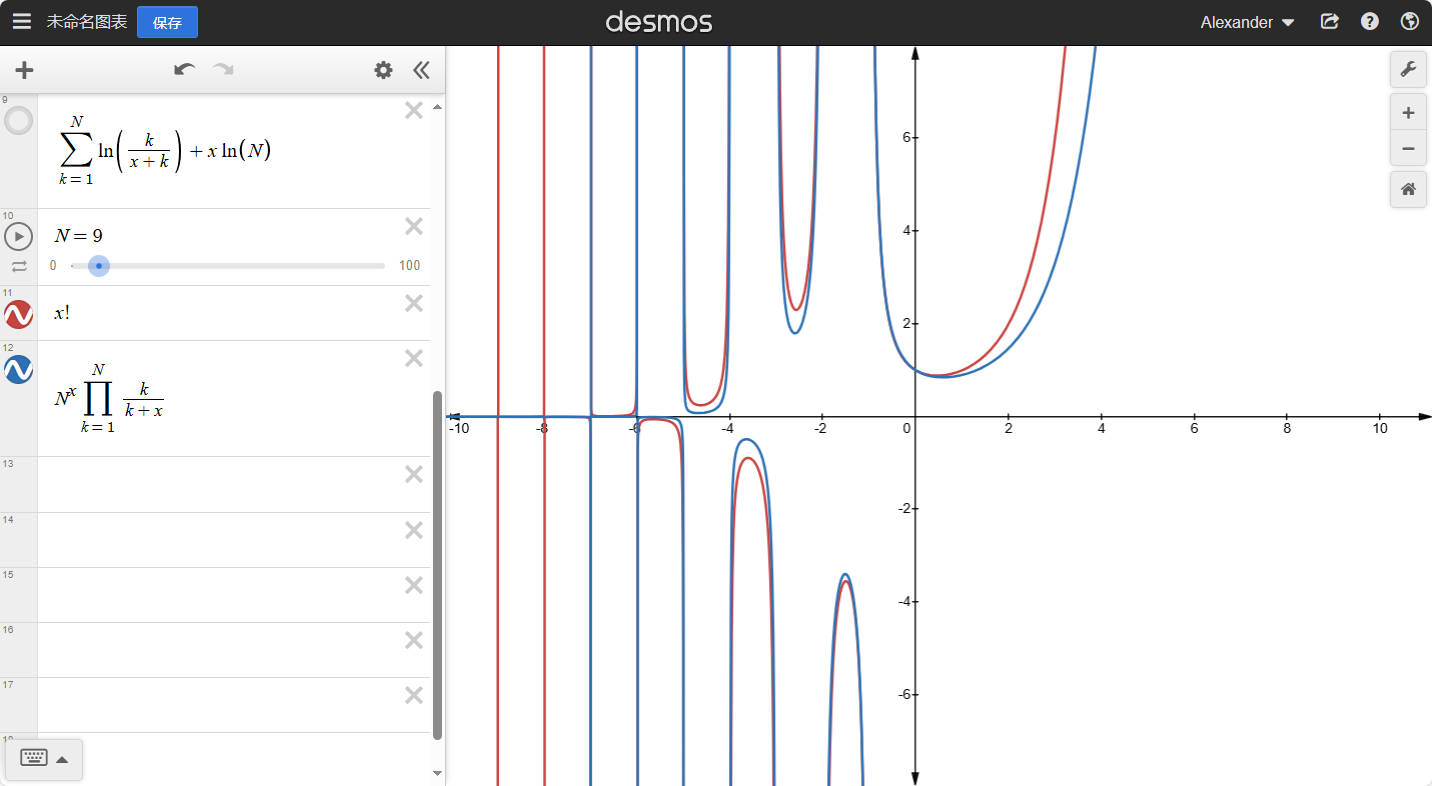
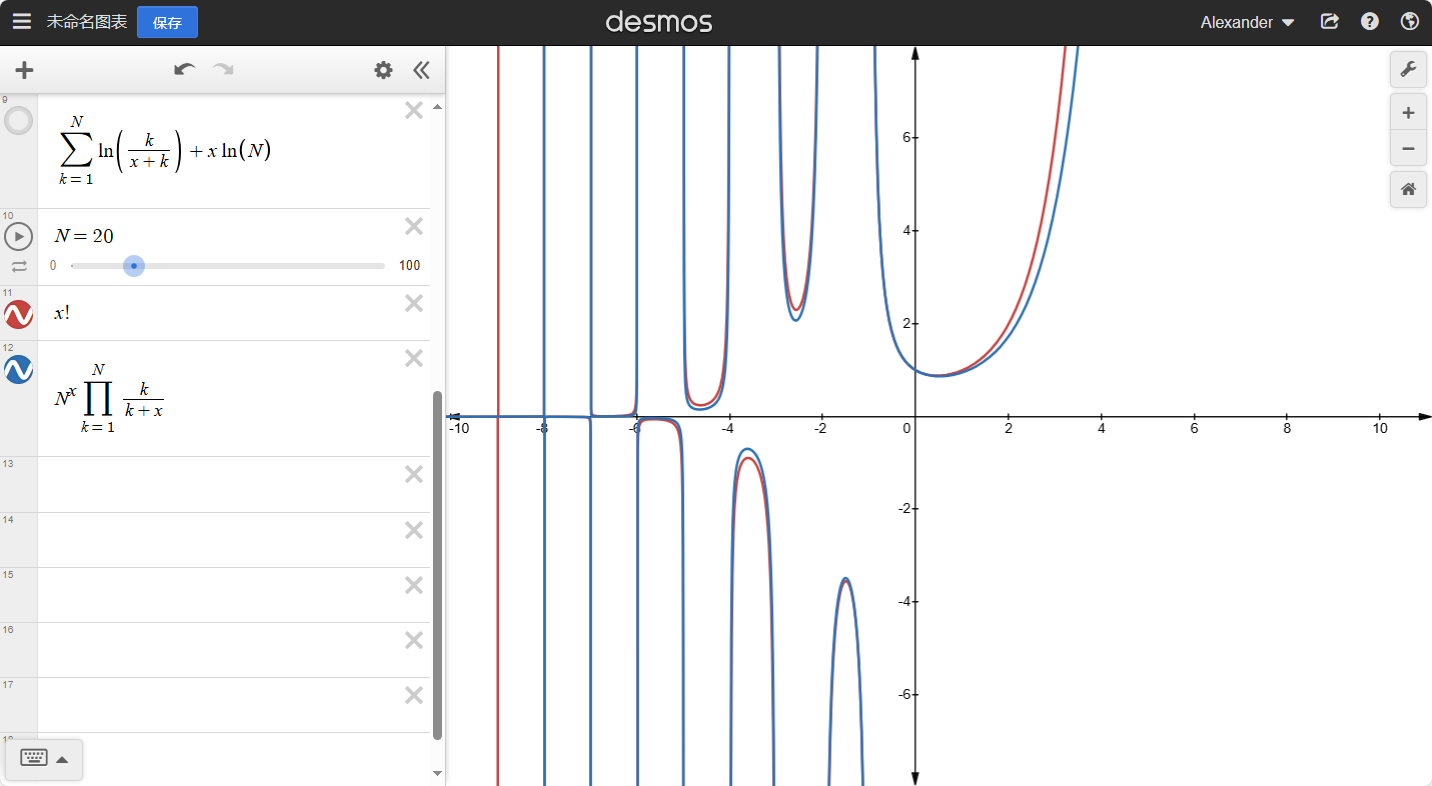
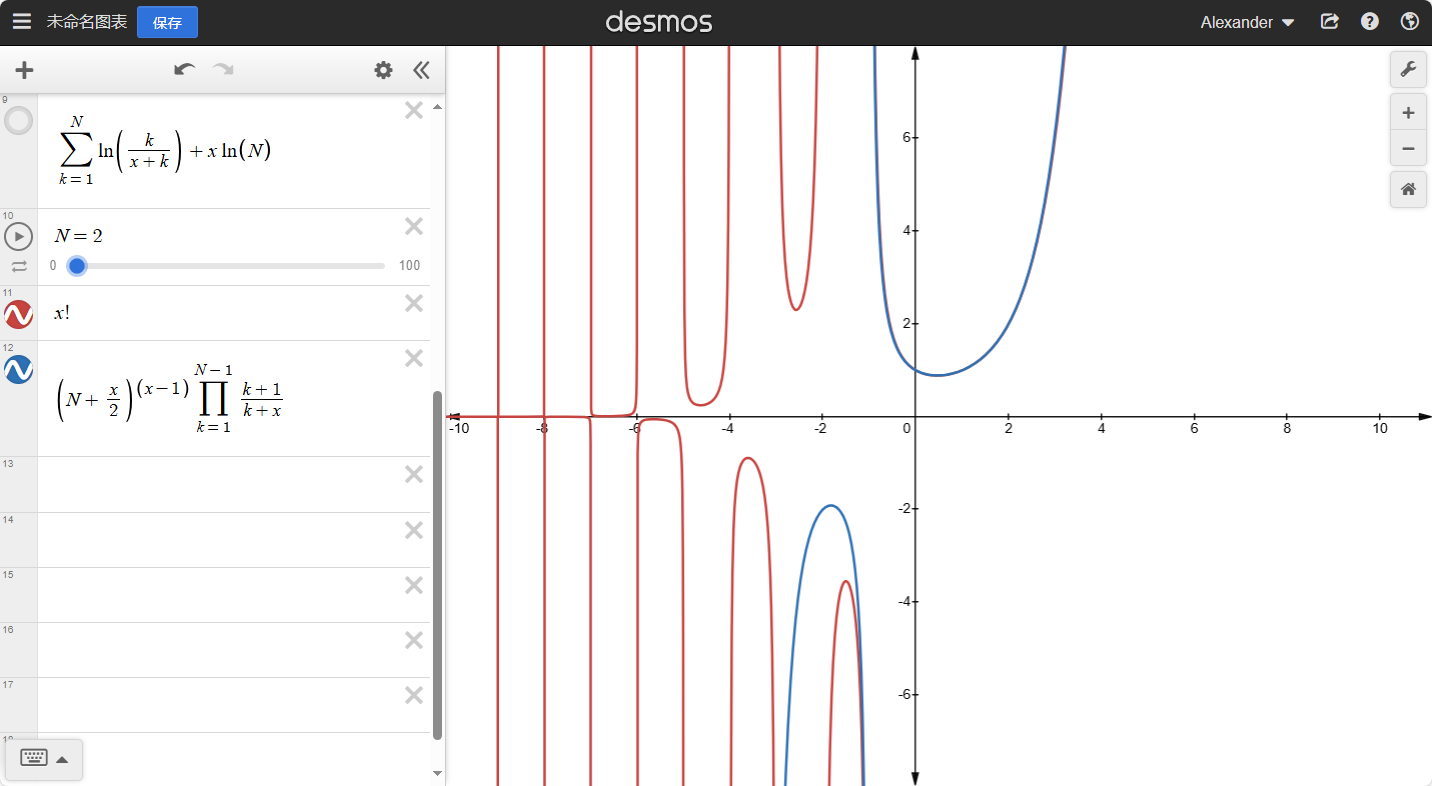
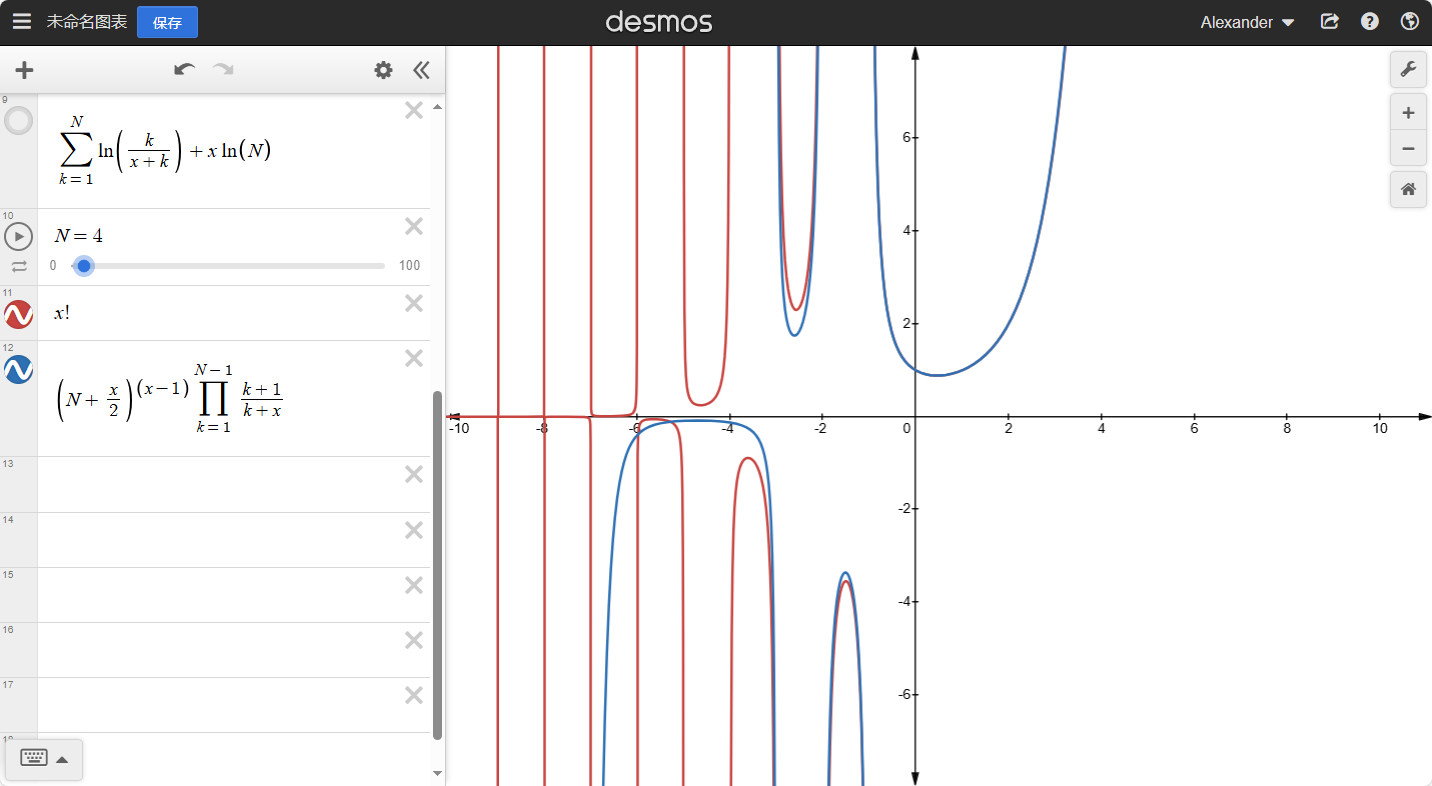
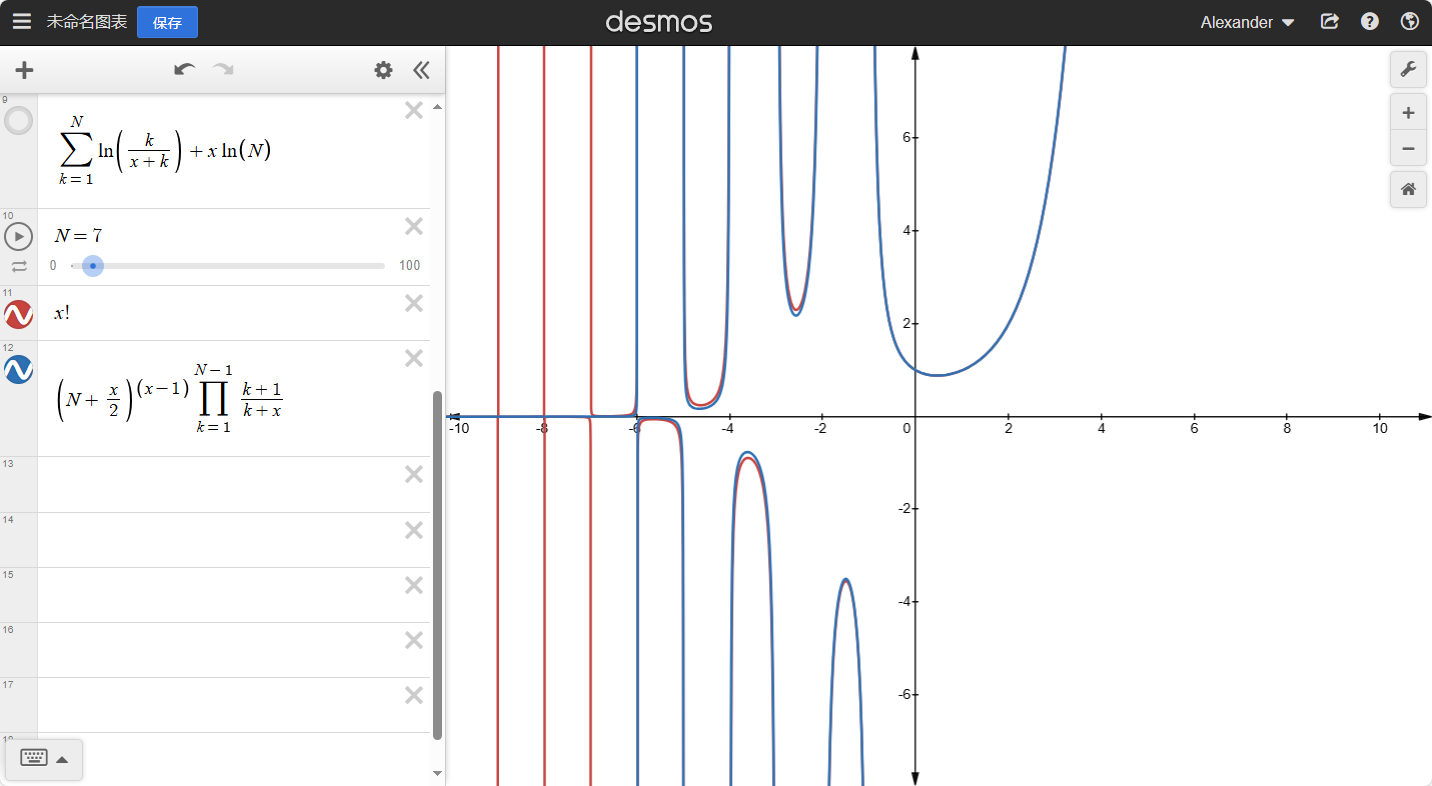
我们可以知道:当x越大时,整个函数的坡度会越小。如果我们去任意大的整数N,那么就有:
H(N)≈H(N+1)≈H(N+2)≈...
也就是:H(N)≈H(N+x),其中x是任意小的数。如果N→∞就有:
N→∞limH(N+x)−H(N)=0N→∞limH(N+x)−k=1∑Nk1=0N→∞limH(x)+k=1∑Nx+k1−k=1∑Nk1=0H(x)=N→∞limk=1∑N−x+k1+k=1∑Nk1H(x)=k=1∑∞(k1−x+k1)
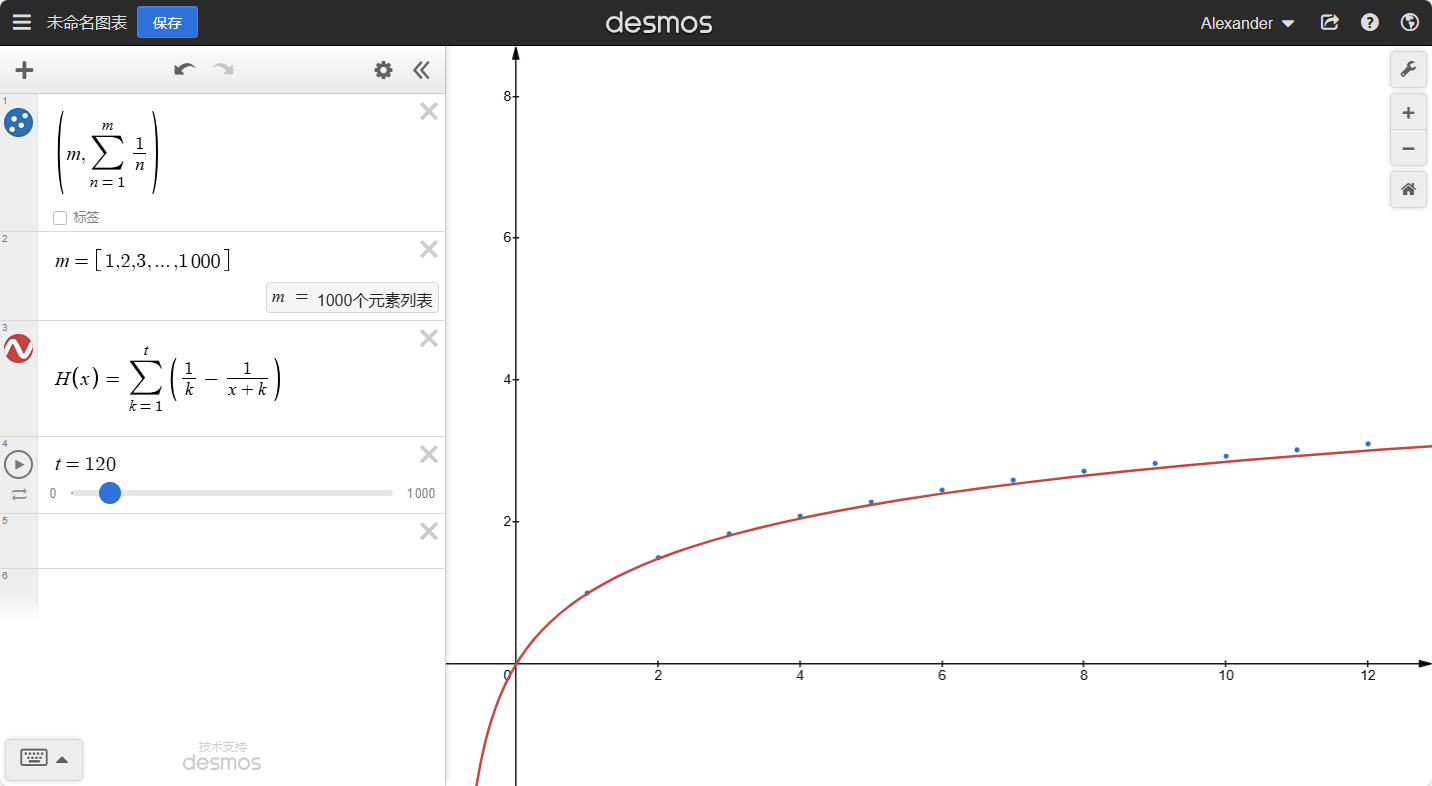
我们来看看最后的图像:




Part2
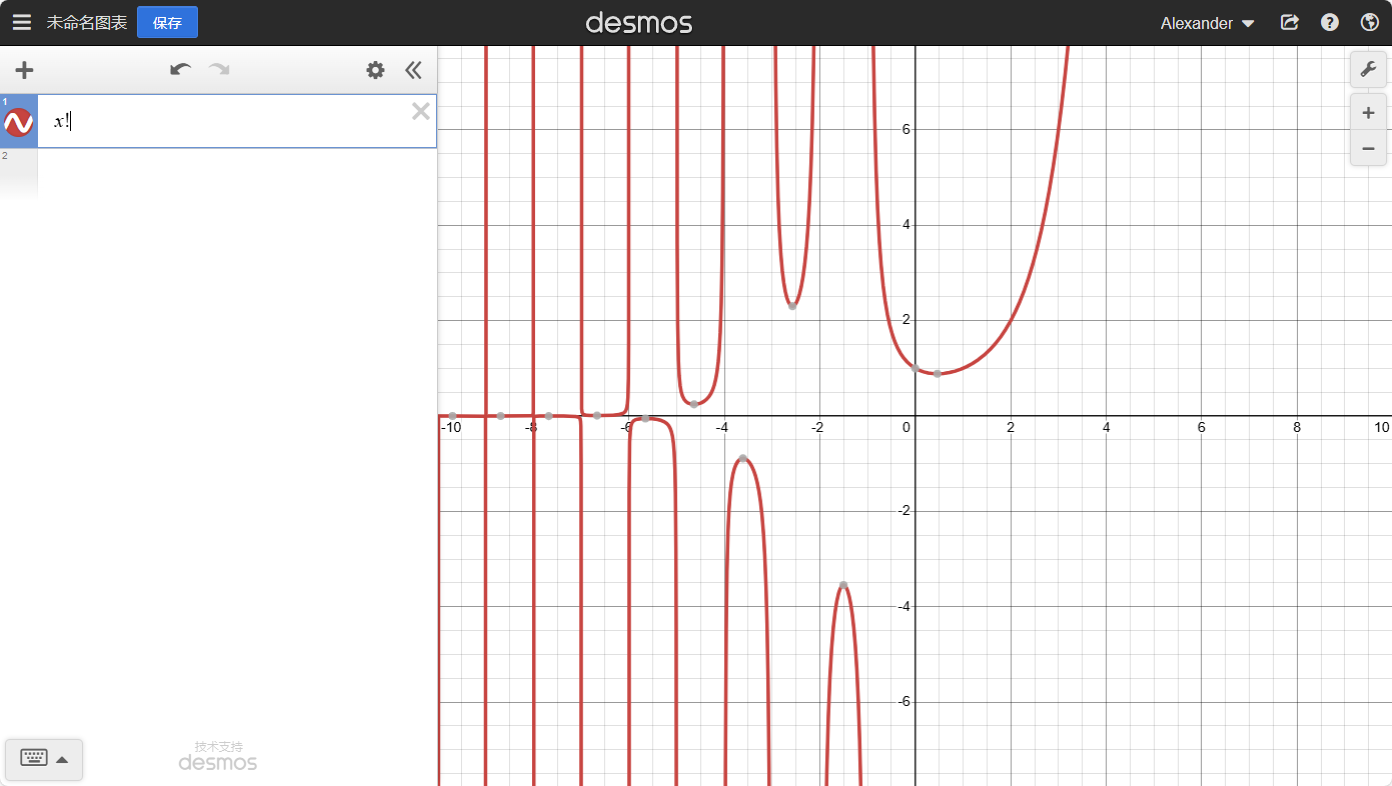
第一节:阶乘的引入
看看下面这个式子:x!=1×2×3×...×x,这就是阶乘函数。第一眼看上去,这个图像的函数应该是一些散点。
我们来看看这个函数的图像:

这个函数并不是我们想得那样,而是一个光滑的函数,这就说明:阶乘是可以被扩充的。那我们来尝试一下。
第二节:扩充阶乘函数
首先我们可以轻松得到下面几个式子:
x!=1×2×3×...×xx!=(x−1)!x(x+k)!=x!n=1∏k(x+n)
可是我们对乘法并不熟悉,于是我们尝试把他变成加法。这里还是那个强大的工具:对数。
ln(x!)=n=1∑xlnnln(x!)=ln(x−1)!+lnxln(x+n)!=ln(x!)+k=1∑nln(x+k)
为了方便叙述,我们定义L(x)=ln(x!),于是上述式子就可以简述成:
L(x)=n=1∑xlnnL(x)=L(x−1)+lnxL(x+n)=L(x)+k=1∑nln(x+k)
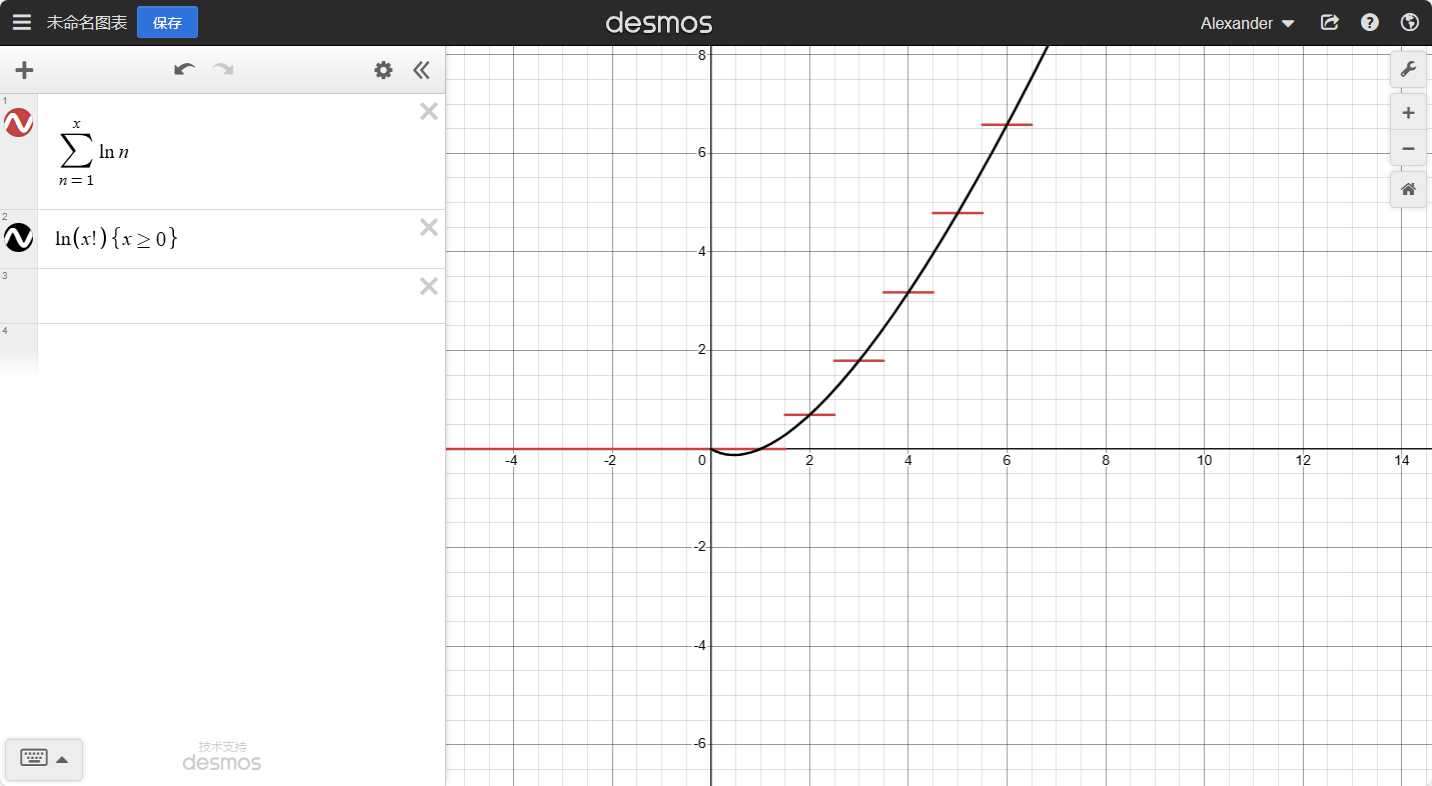
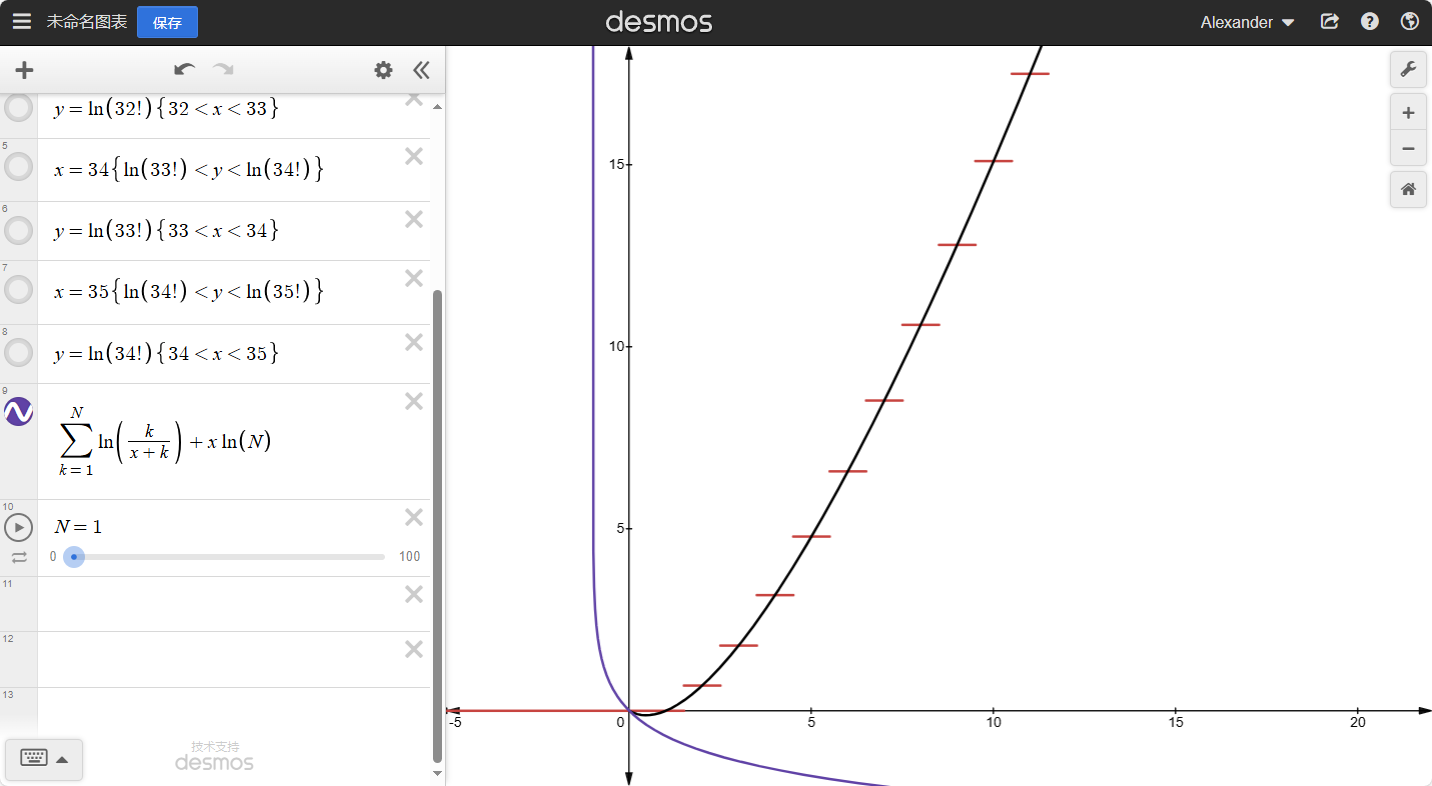
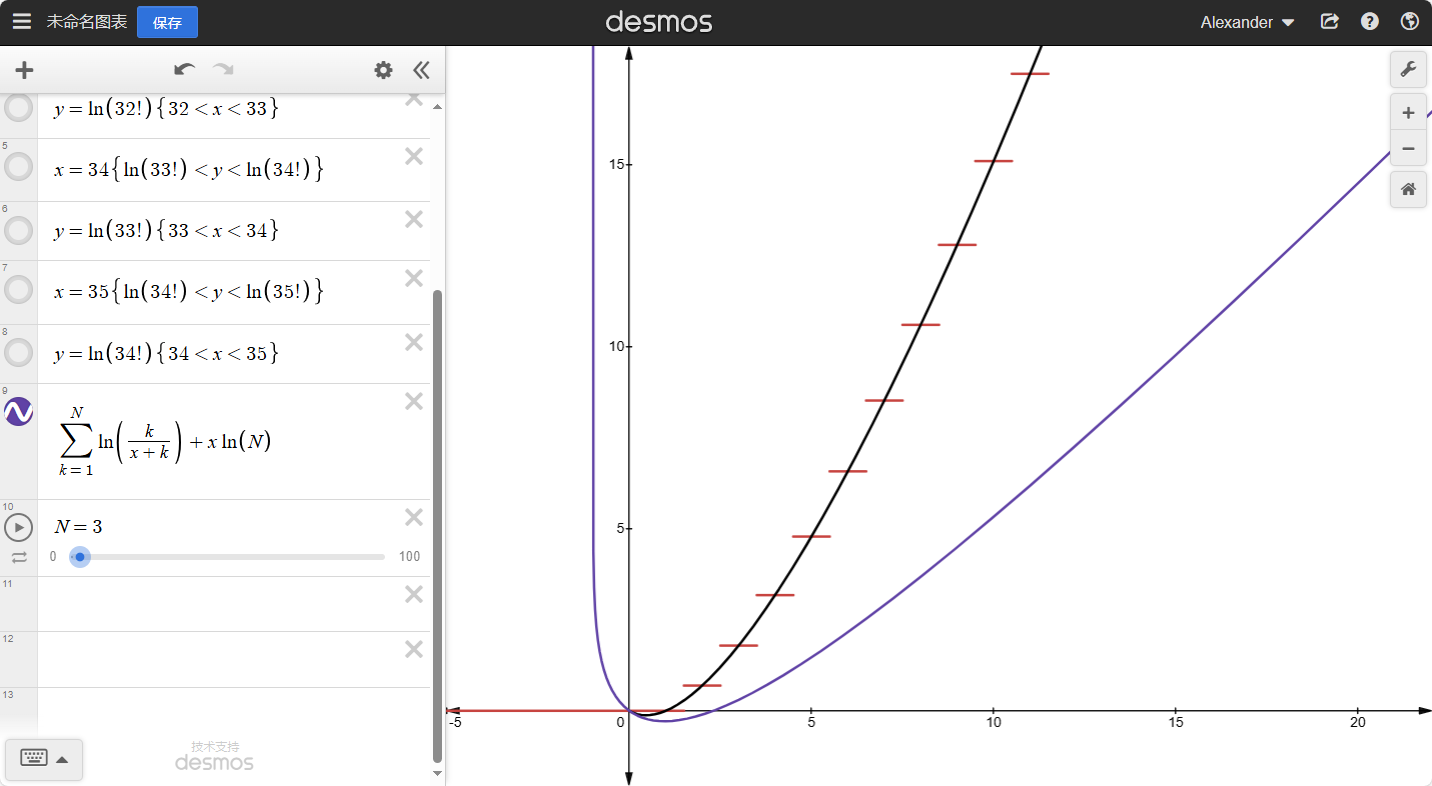
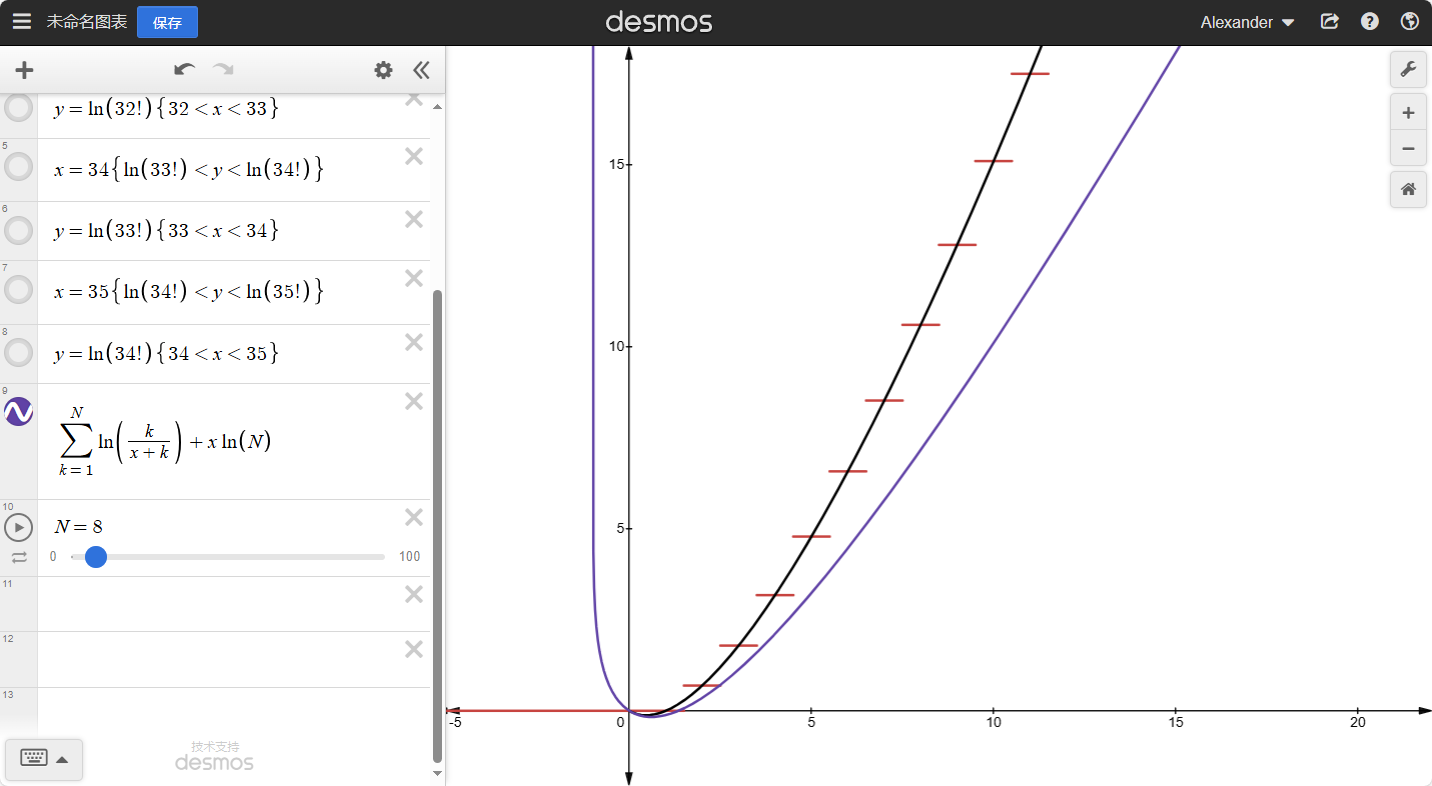
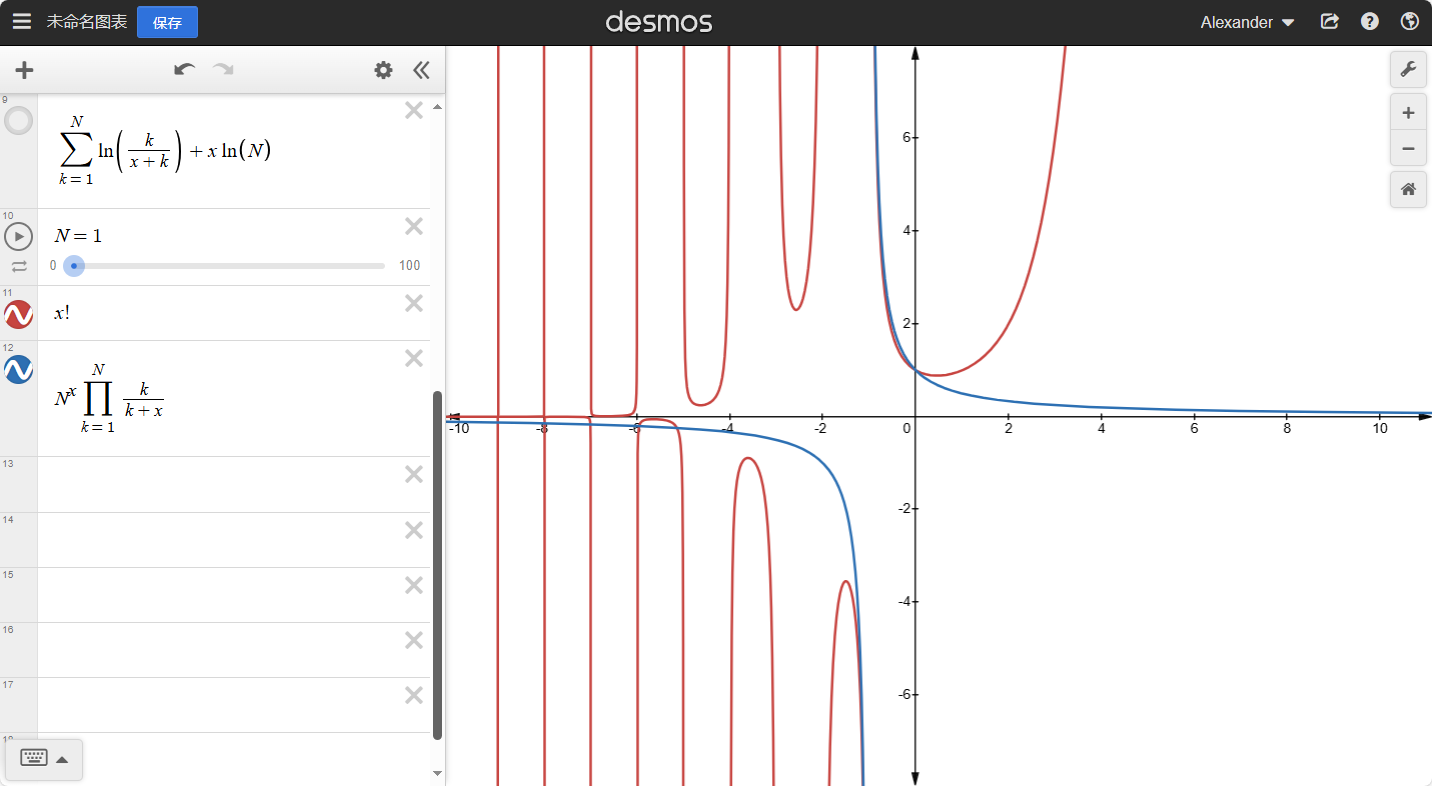
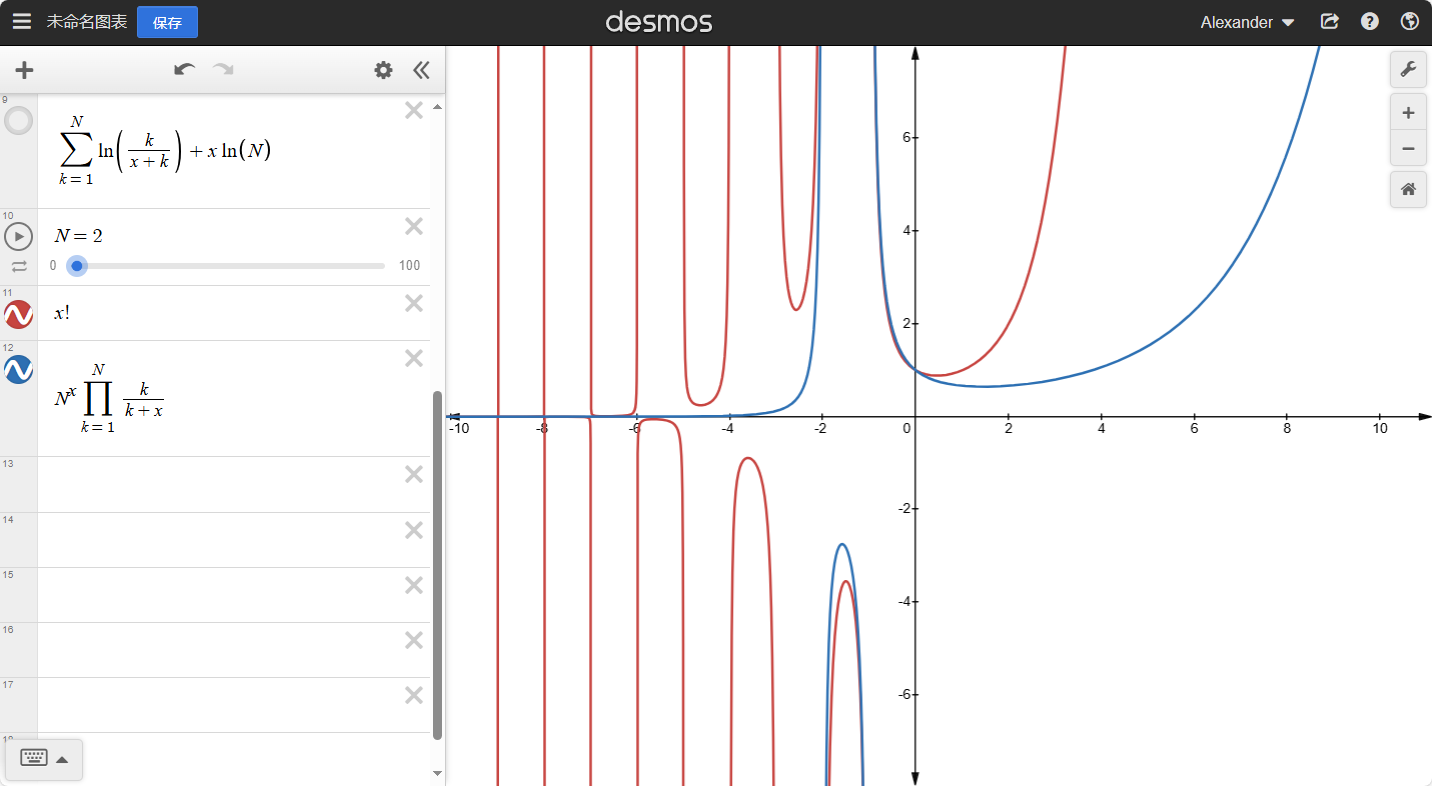
我们来绘制一下L(x)的 图像

其中交点处便是函数L(x)的图像。我们发现他比x!平缓了许多。而且越往后,这个函数的图像会越接近一条直线。
假设我们拉到了x=N,N为任意大整数,那么,我们就可以得到:L(N)−L(N−1)=lnN,以此类推

所以我们就有:ln(N)≈ln(N+1)≈ln(N+2)≈...,特别的,当N→∞时,k为相当小的整数,我们有:
N→∞limln(N+k)−ln(N)=N→∞limln(NN+k)=N→∞limln(1+Nk)=0
现在我们回来:
L(x+N)=L(N)+k=1∑xln(N+k)L(x+N)≈k=1∑Nlnk+xln(N)L(x)≈k=1∑Nlnk−k=1∑Nln(x+k)+xln(N)L(x)≈k=1∑Nln(x+kk)+xln(N)
这样我们就得到到了这样一个式子,从直觉上来判断,我们就可以得到:令N→∞,有:
L(x)=N→∞limk=1∑Nln(x+kk)+xln(N)
Proof:
L(x+N)=L(N)+k=1∑xln(N+k)L(x+N)=L(N)+k=1∑x(ln(N)+ln(N+k)−ln(N))L(x+N)=L(N)+k=1∑xln(N)+k=1∑x(ln(N+k)−ln(N))N→∞limL(x+N)−L(N)−k=1∑xln(N)=N→∞limk=1∑x(ln(NN+k))N→∞limL(x+N)−L(N)−k=1∑xln(N)=0N→∞limL(x+N)−L(N)−xln(N)=0N→∞limL(x)+k=1∑Nln(x+k)−L(N)−xln(N)=0N→∞limL(x)+k=1∑Nln(x+k)−k=1∑Nln(k)−xln(N)=0L(x)+N→∞limk=1∑Nln(x+k)−k=1∑Nln(k)−xln(N)=0L(x)=N→∞lim−k=1∑Nln(x+k)+k=1∑Nln(k)+xln(N)L(x)=N→∞limk=1∑Nln(x+kk)+xln(N)
Q.E.D.
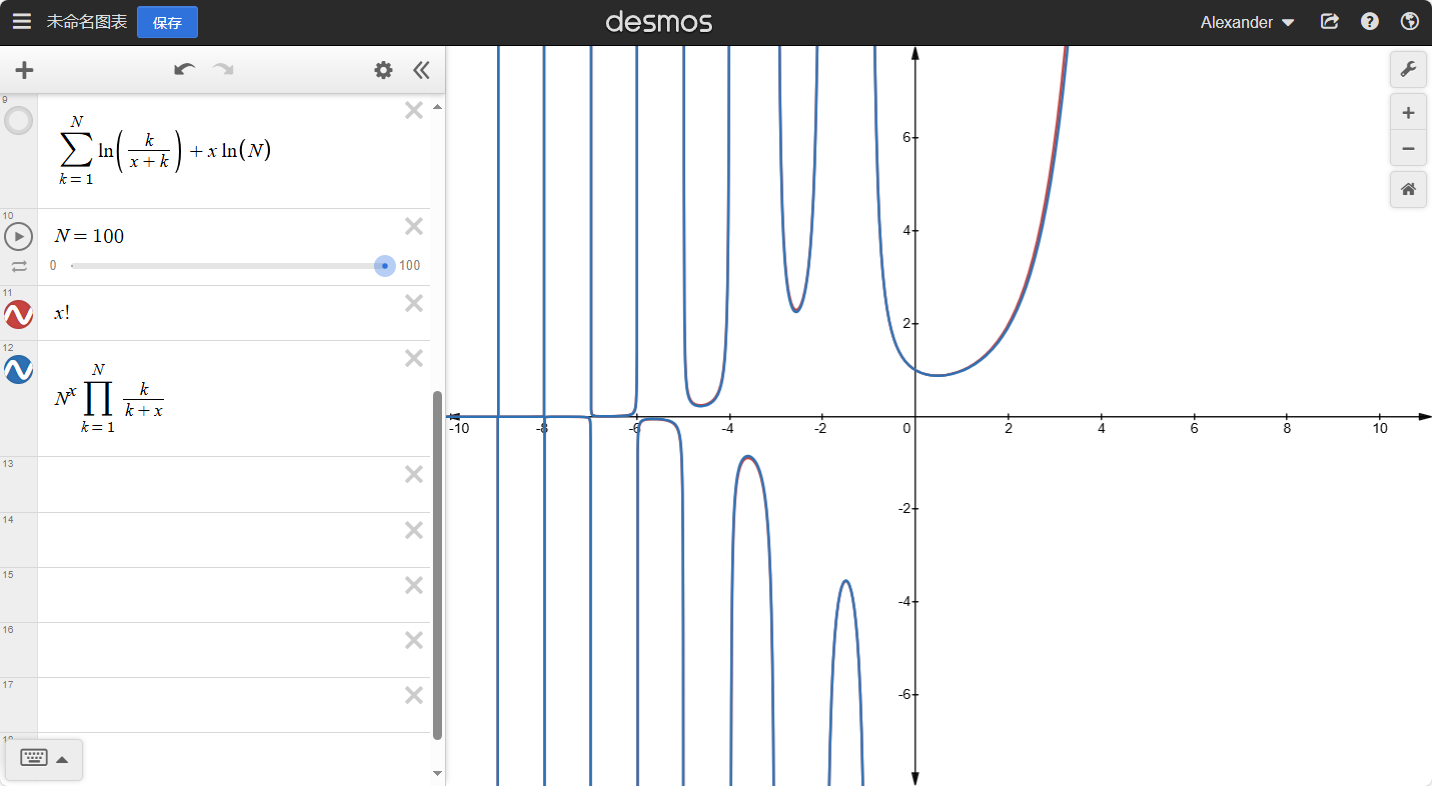
现在我们就有了关于L(x)的另外一个表达式,画一下图像看一看。





所以:L(x)=limN→∞∑k=1Nln(x+kk)+xln(N)是成立的。从图像上我们可以知道,这对任何数都是成立的。
别忘了,L(x)=ln(x!)。所以我们有:
x!=N→∞lime∑k=1Nln(x+kk)+xln(N)x!=N→∞limNxk=1∏Nx+kk
画出x!的图像,于是我们就得到了:






至此我们就把x!扩充到了实数。
第三节:历史了解
我们为这个成果感到高兴,但最早是欧拉(Euler)的朋友:丹尼尔·伯努利(Daniel Bernoulli)于1729.10.6第一个发表的扩展x!。而欧拉在1729.10.19发表了我们推导出来的式子。当时丹尼尔·伯努利发表的式子为下列式子,然而事实上,这个式子收敛的更快,但取而代之的是复杂度(不会证······)。
n→∞lim(N+2x)x−1k=1∏N−1x+kk+1






我们发现欧拉的解当x=100时还没有伯努利的解x=11时好,但是这个式子还是以欧拉出名,为什么呢?
原因是因为欧拉的工作更为深入:他追求的是找到一个使用积分而非无穷乘积的表达式。
不出所料,在仅仅过了几个月后,欧拉在1730.1.8发表了另一个解(我肯定是不会证的QAQ):
∫01(−ln(t))xdt or ∫0∞txe−tdt
调和级数与阶乘的关系
我们对阶乘函数的对数求导:
dxdln(x!)=dxd(N→∞limk=1∑Nln(x+kk)+xln(N))=N→∞limk=1∑Ndxdln(x+kk)+dxdxln(N)=N→∞limk=1∑N(dxdln(k)−dxdln(x+k))+ln(N)=N→∞limk=1∑N−x+k1+ln(N)
到这里,仔细观察可以发现:调和级数的函数为H(x)=∑k=1∞(k1−x+k1),那么这两者就有莫名的关系。我们通过添项的方式来凑出H(x)。
dxdln(x!)=dxd(N→∞limk=1∑Nln(x+kk)+xln(N))=N→∞limk=1∑Ndxdln(x+kk)+dxdxln(N)=N→∞limk=1∑N(dxdln(k)−dxdln(x+k))+ln(N)=N→∞limk=1∑N−x+k1+ln(N)=N→∞limk=1∑Nk1+k=1∑N−x+k1−k=1∑Nk1+ln(N)=N→∞limk=1∑N(k1−x+k1)−k=1∑Nk1+ln(N)=N→∞limH(x)−H(N)+ln(N)=H(x)−N→∞lim(H(N)−ln(N))
随后我们可以发现:后面的limN→∞(H(N)−ln(N))
不随x的变化而变化,是一个常数。一般把这个常数叫做 “伽马常数(欧拉常数)” 通过计算我们可以得到它等于0.5772161649007153...,用希腊字母 γ 表示,也就是:
γ=N→∞lim(H(N)−ln(N))=0.5772161649007153...
这就有一个意外的发现:阶乘对数的导数等于调和级数减去伽马常数:
dxdln(x!)=H(x)−γ
Part3
Note:
Part3下去我们有些符号要换成更官方的符号,前面的符号为大家做一个铺垫:
Γ函数和阶乘:
Γ(x)=(x−1)!Γ(x)=N→∞limNx−1k=1∏Nx−1+kkΓ(x+1)=xΓ(x)
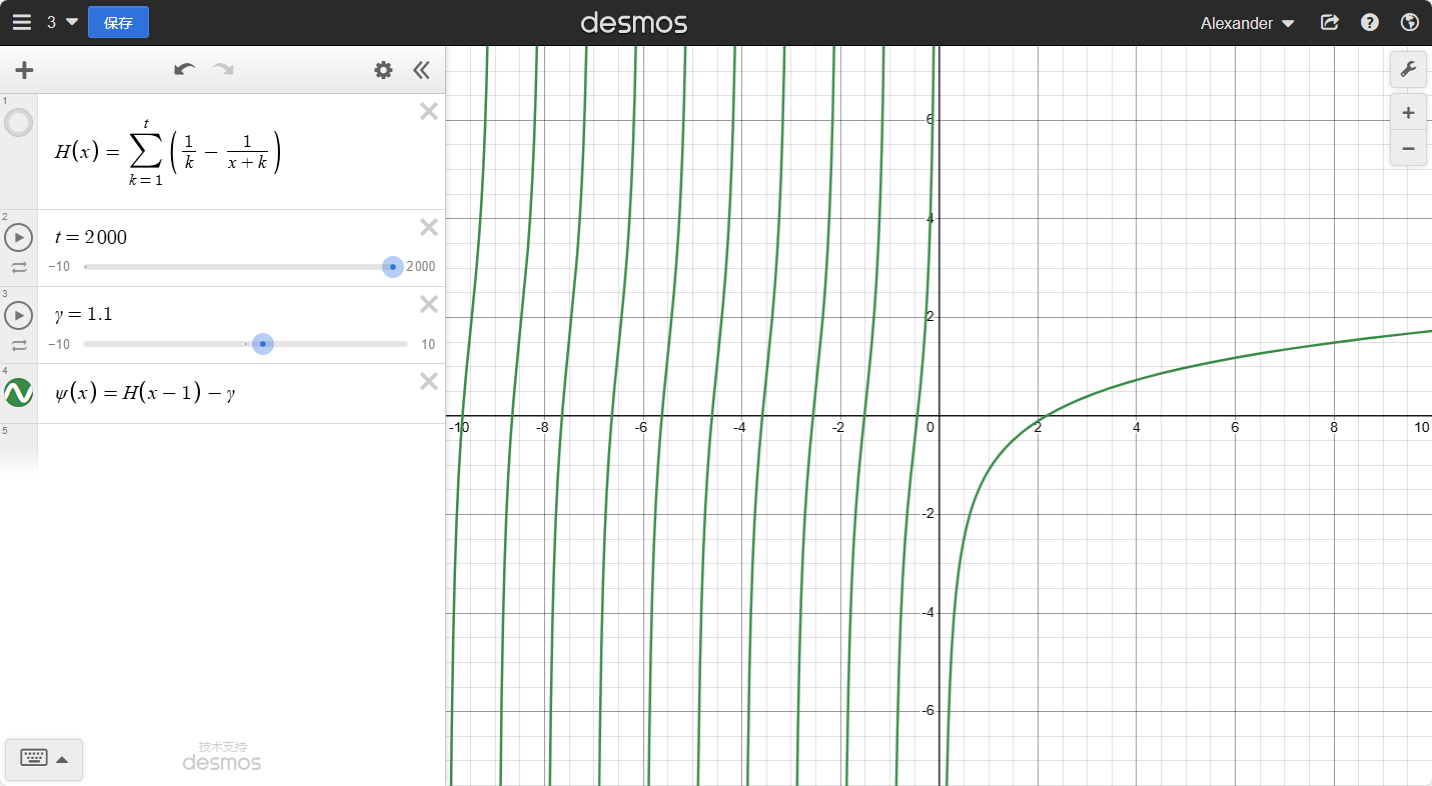
ψ函数和调和级数:
ψ(x)=dxdln(Γ(x))=H(x−1)−γψ(x+1)=ψ(x)+x1
OK!让我们进入主题。
1.ψ(x)与cot(x)

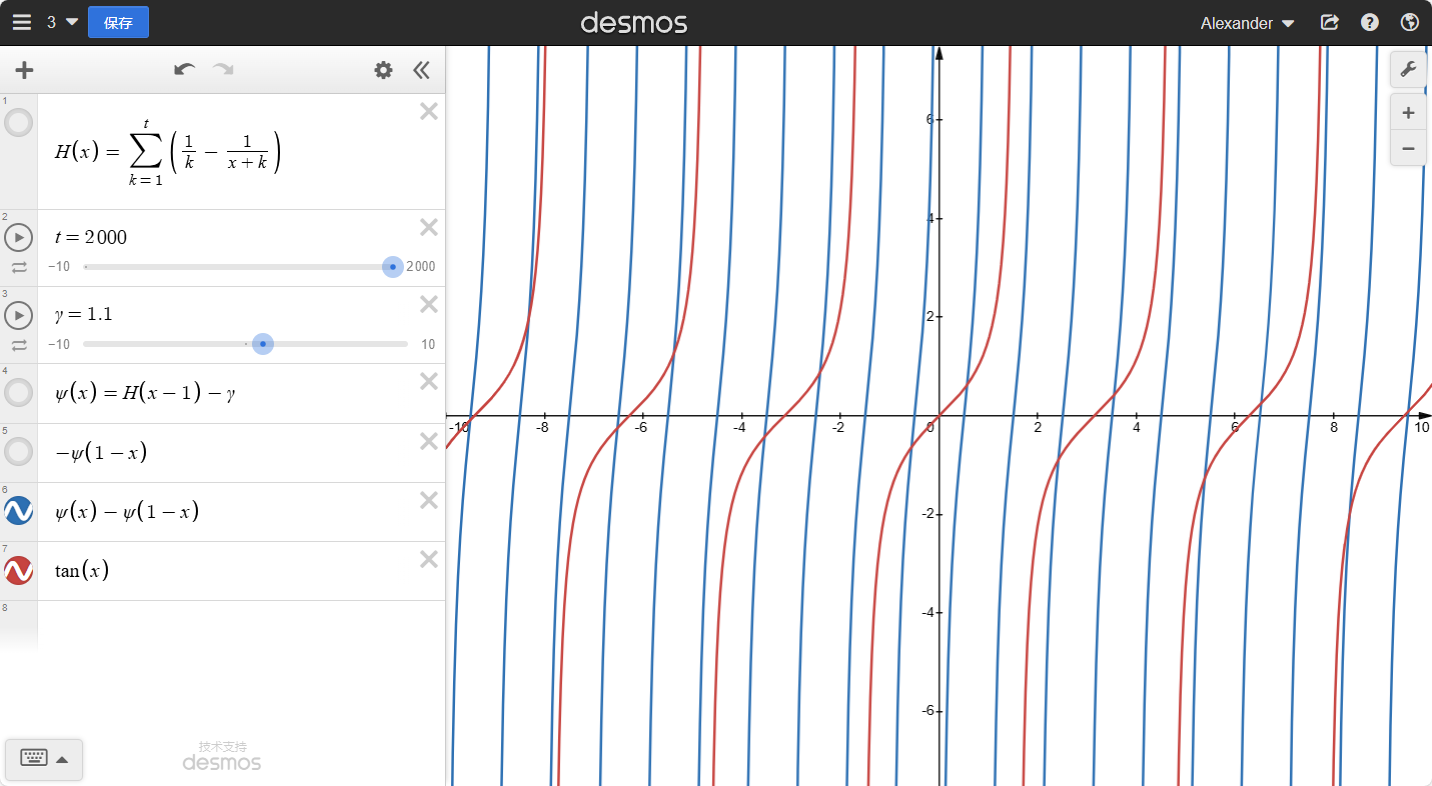
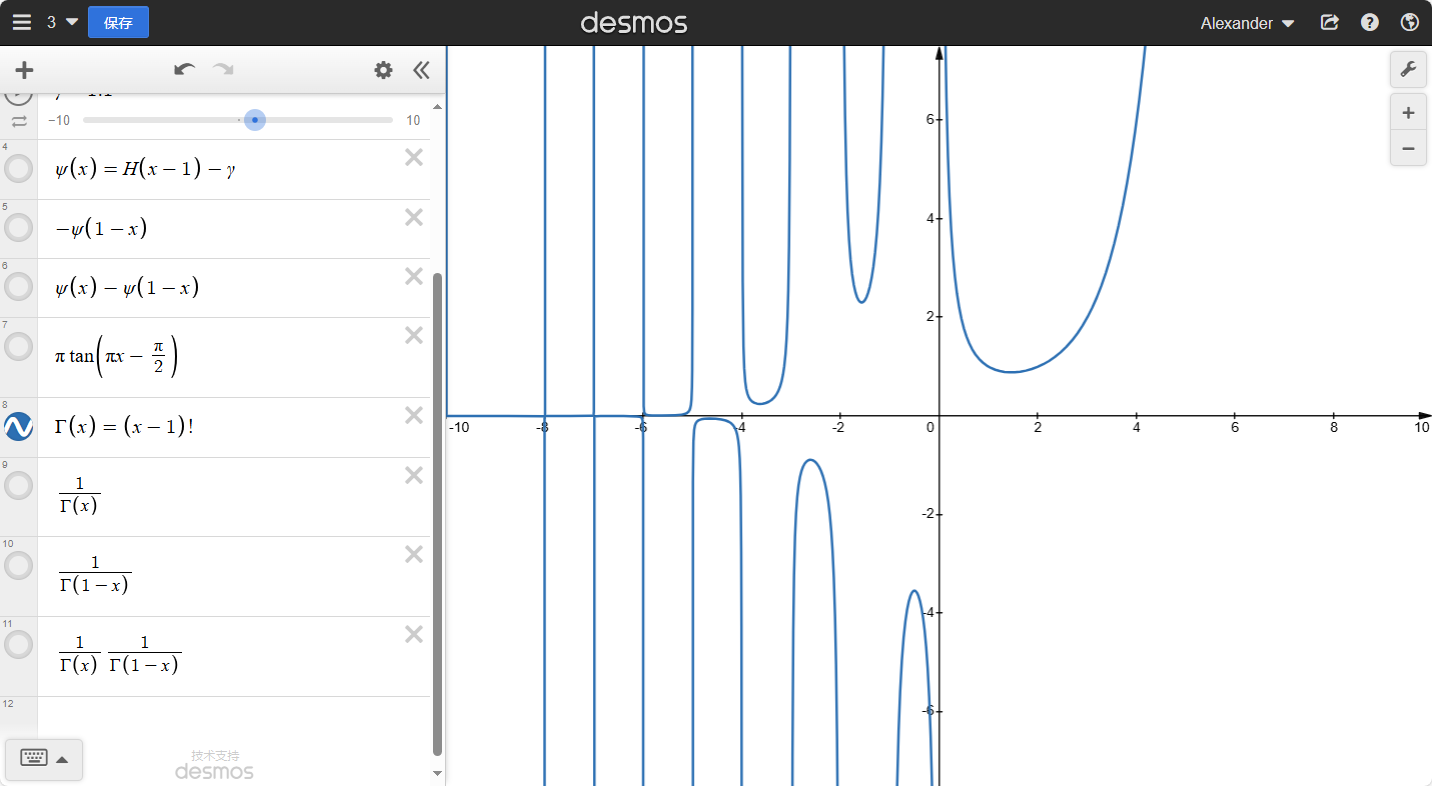
我们可以看到ψ(x)的x负半轴上的函数有点像tan函数。为了我们更好操作,我们让x轴也出现渐近线:−ψ(1−x),

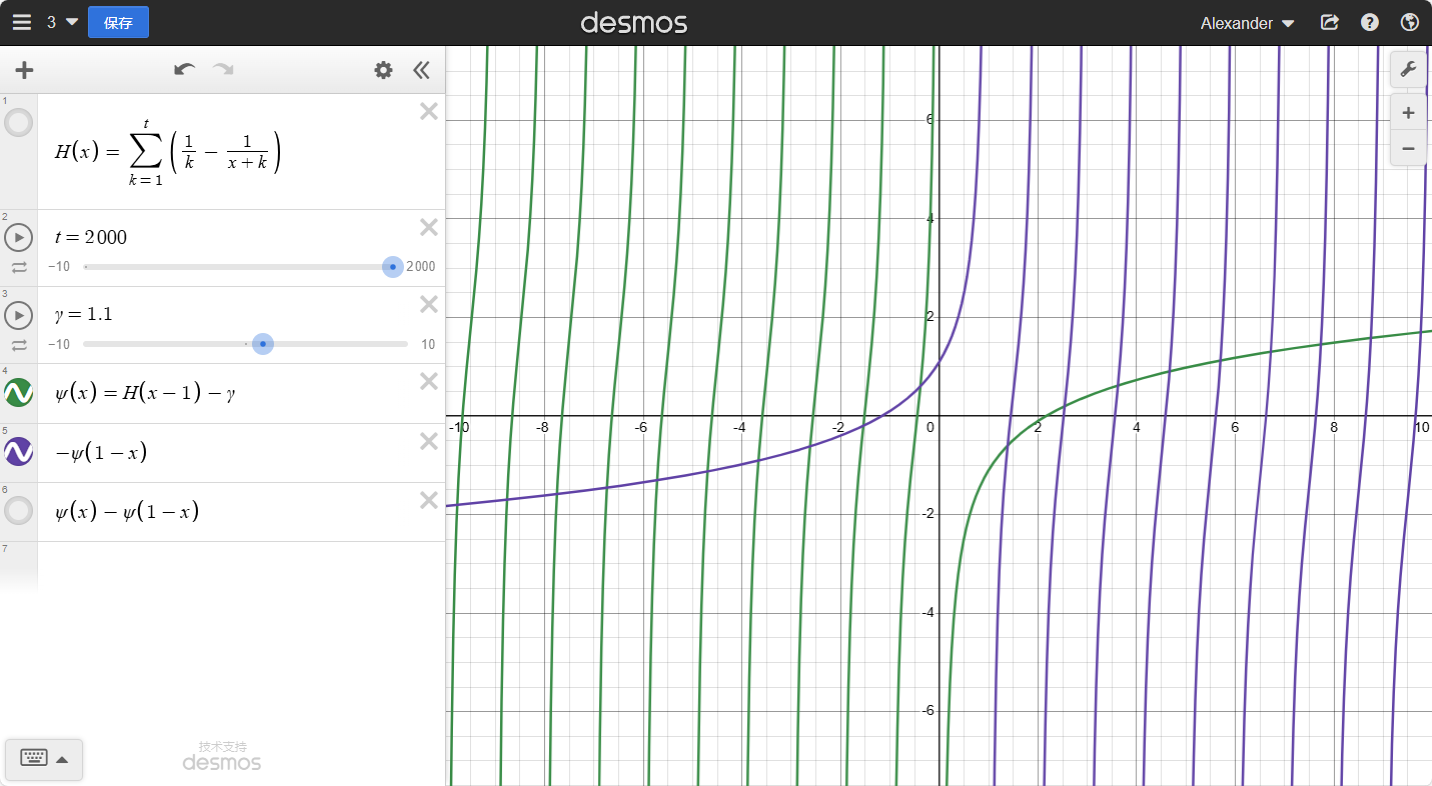
最后我们把这两个函数加起来:

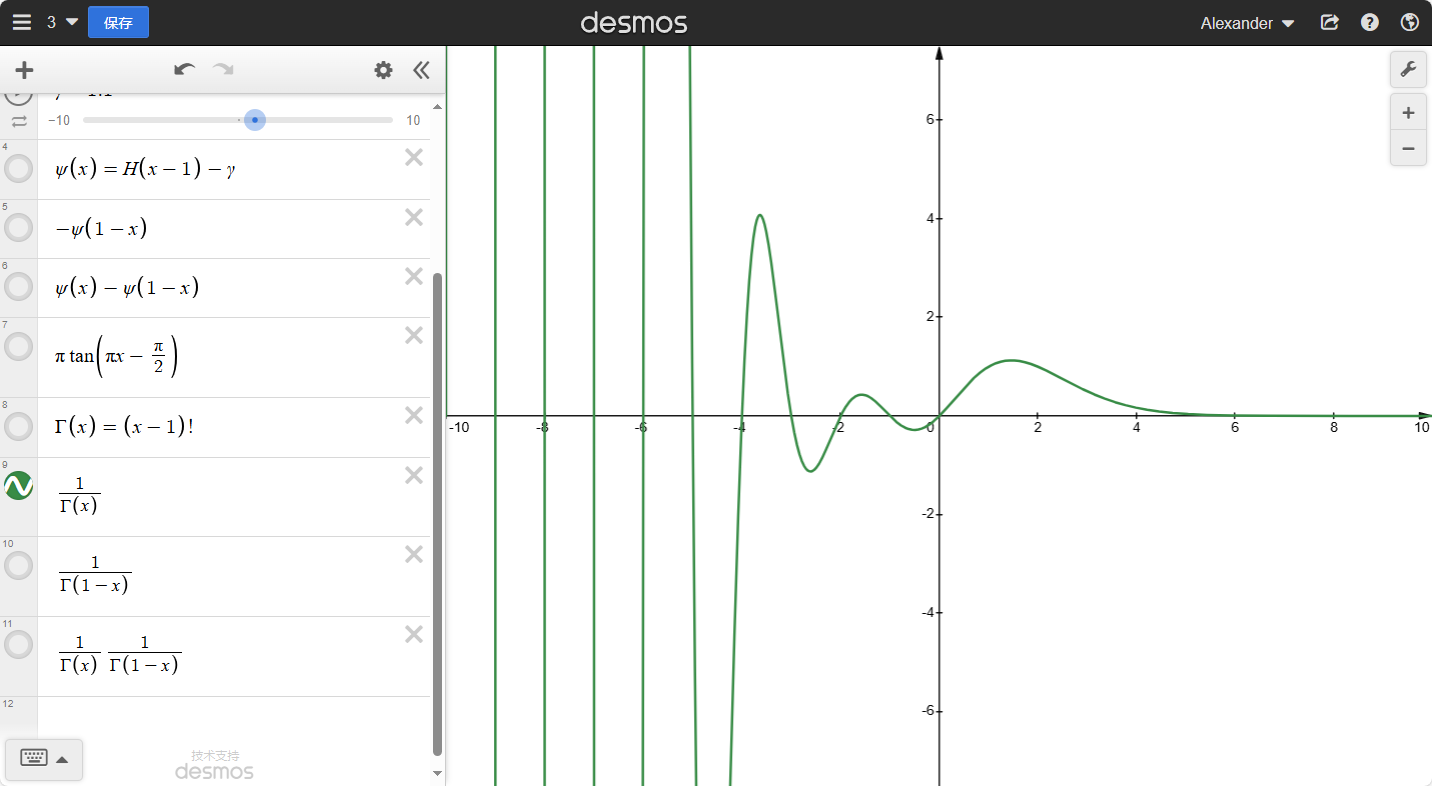
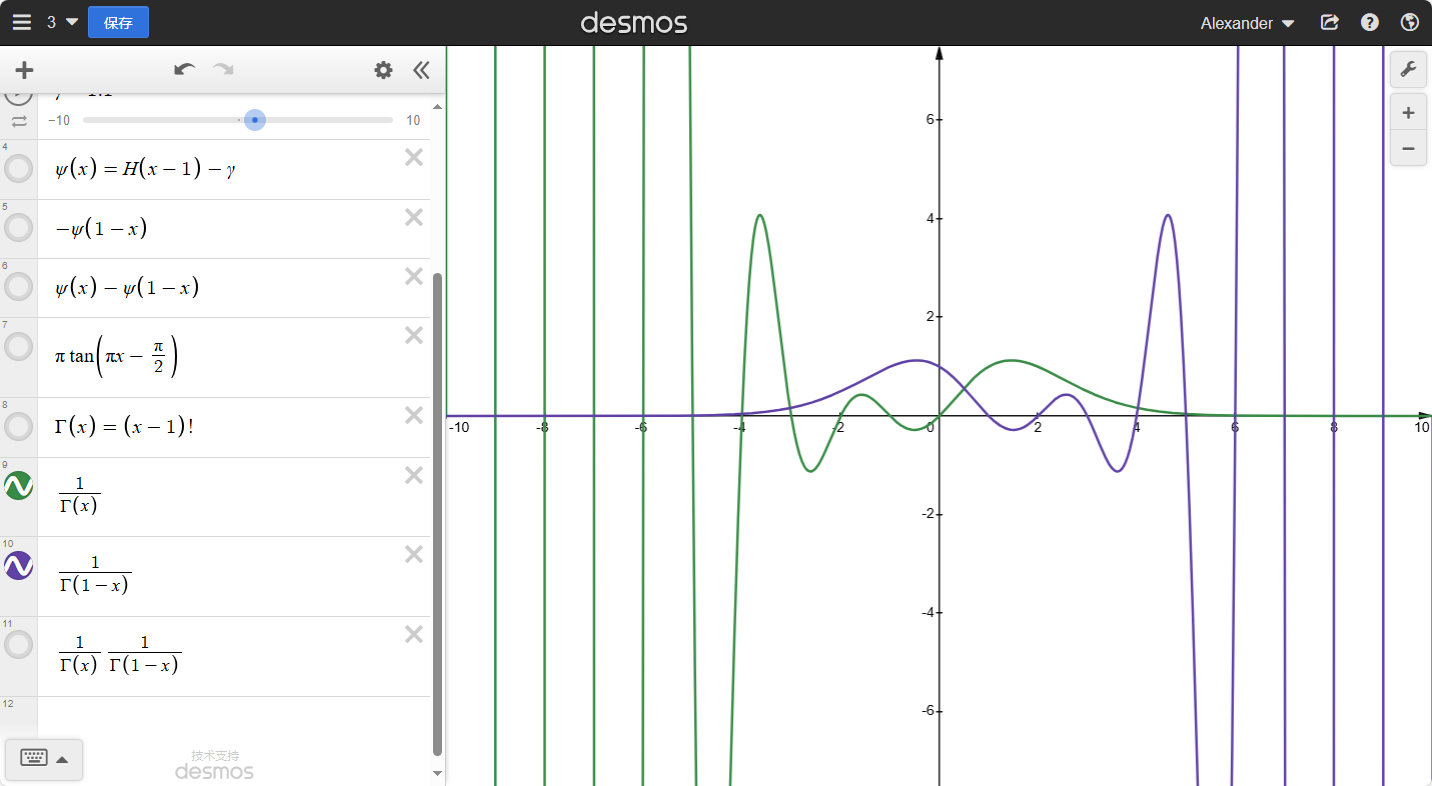
观察一下:真的好像tanx,我们放在一起比对一下:

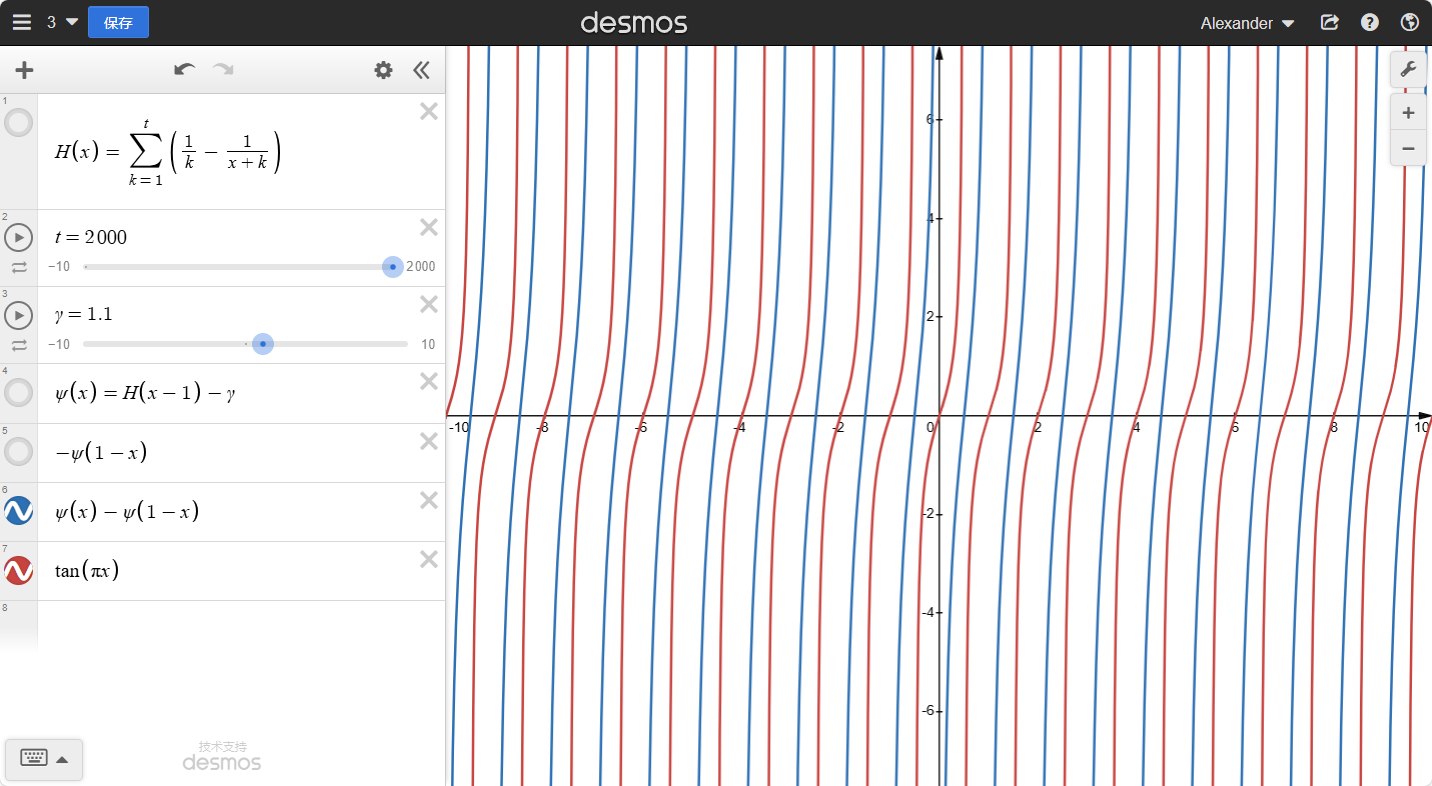
接下来我们做点调整:
1.水平压缩π倍:

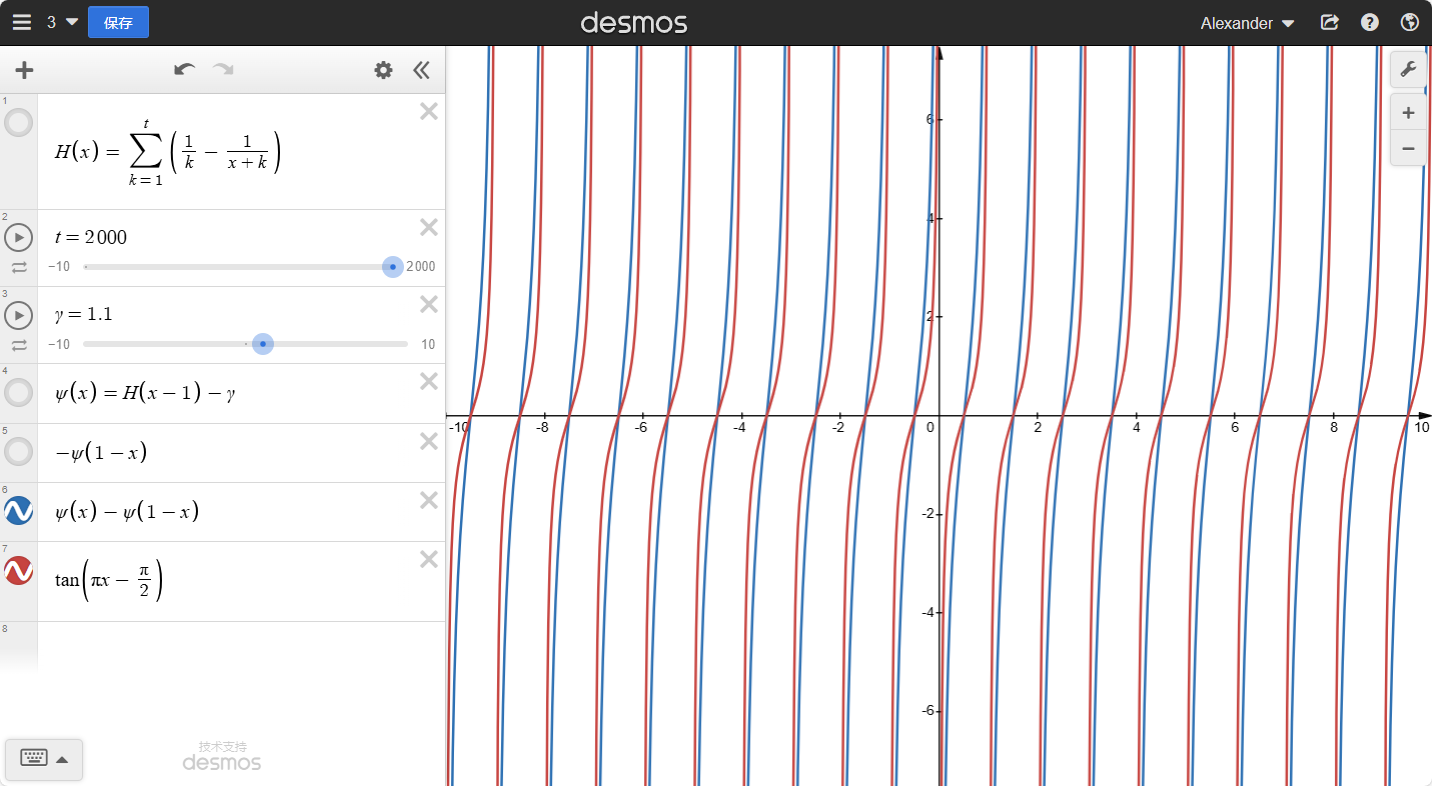
2.右移21个单位:

3.上下拉伸π倍:

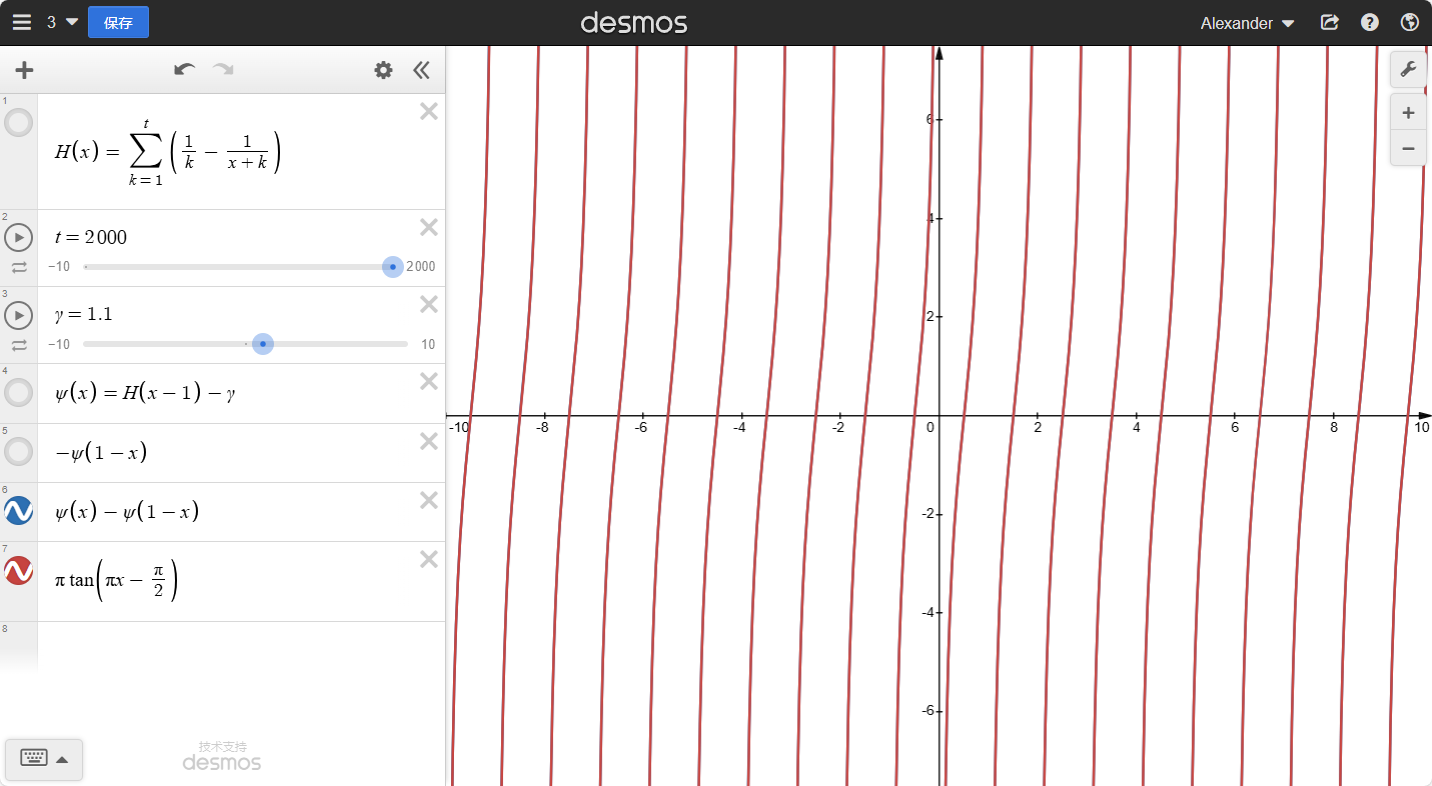
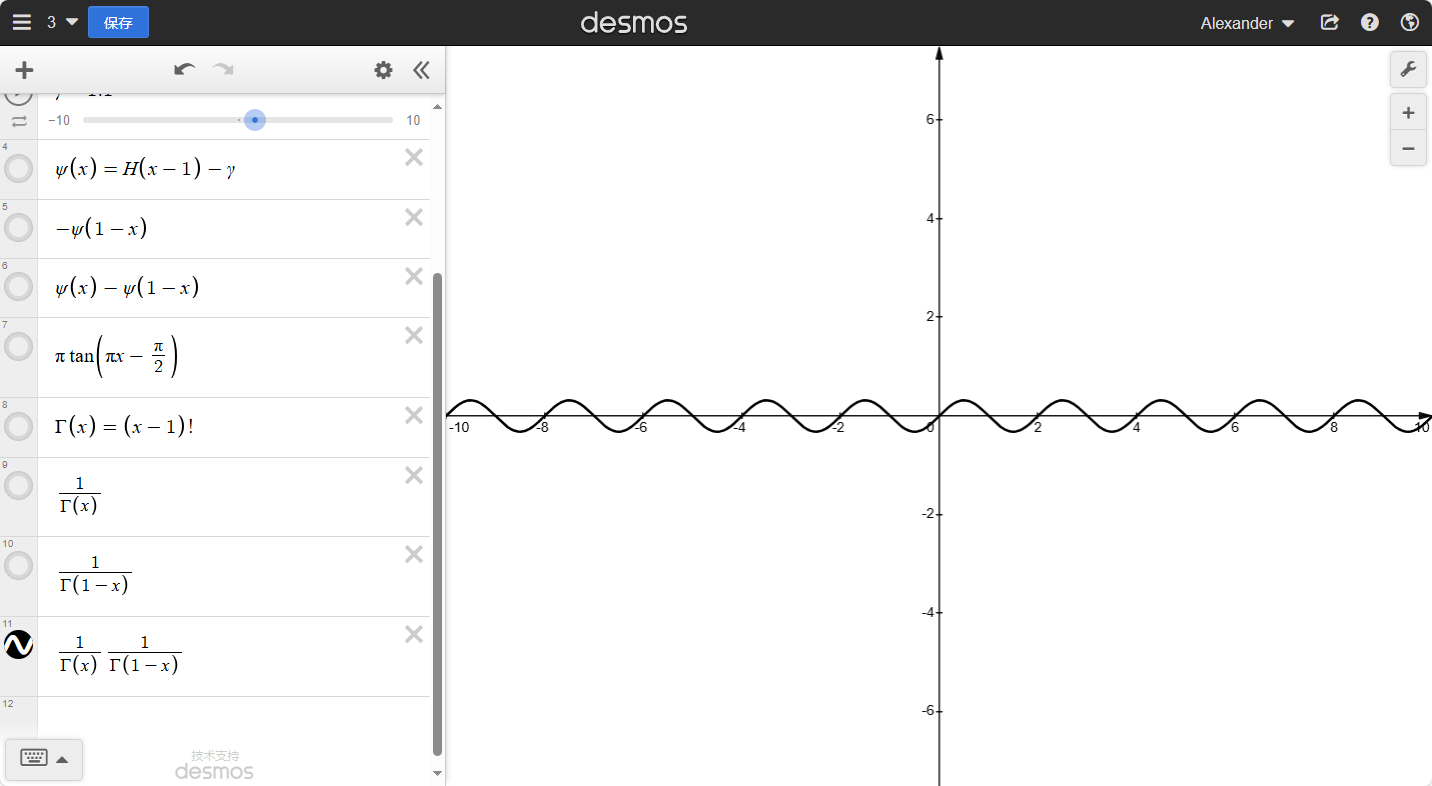
于是我们就可以得到:
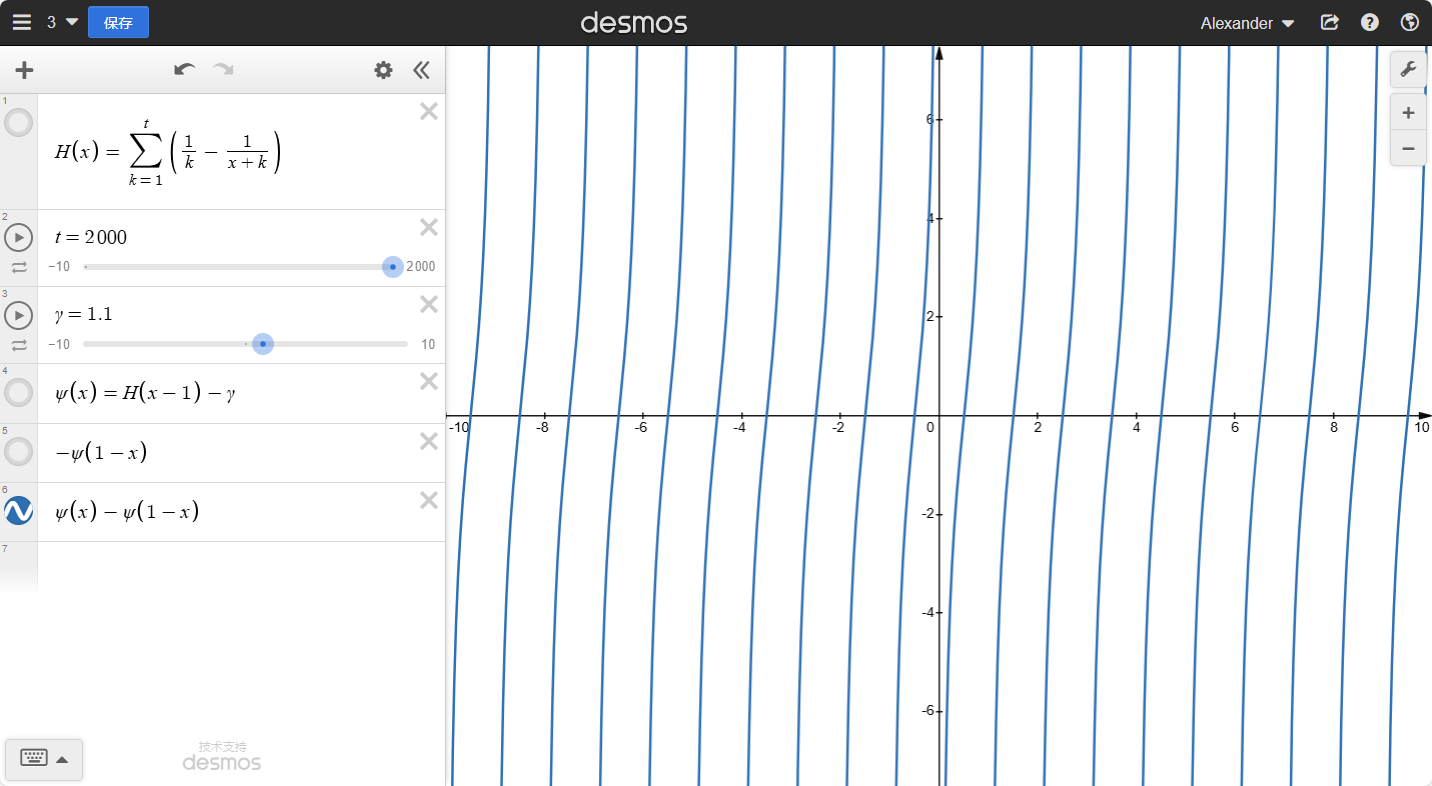
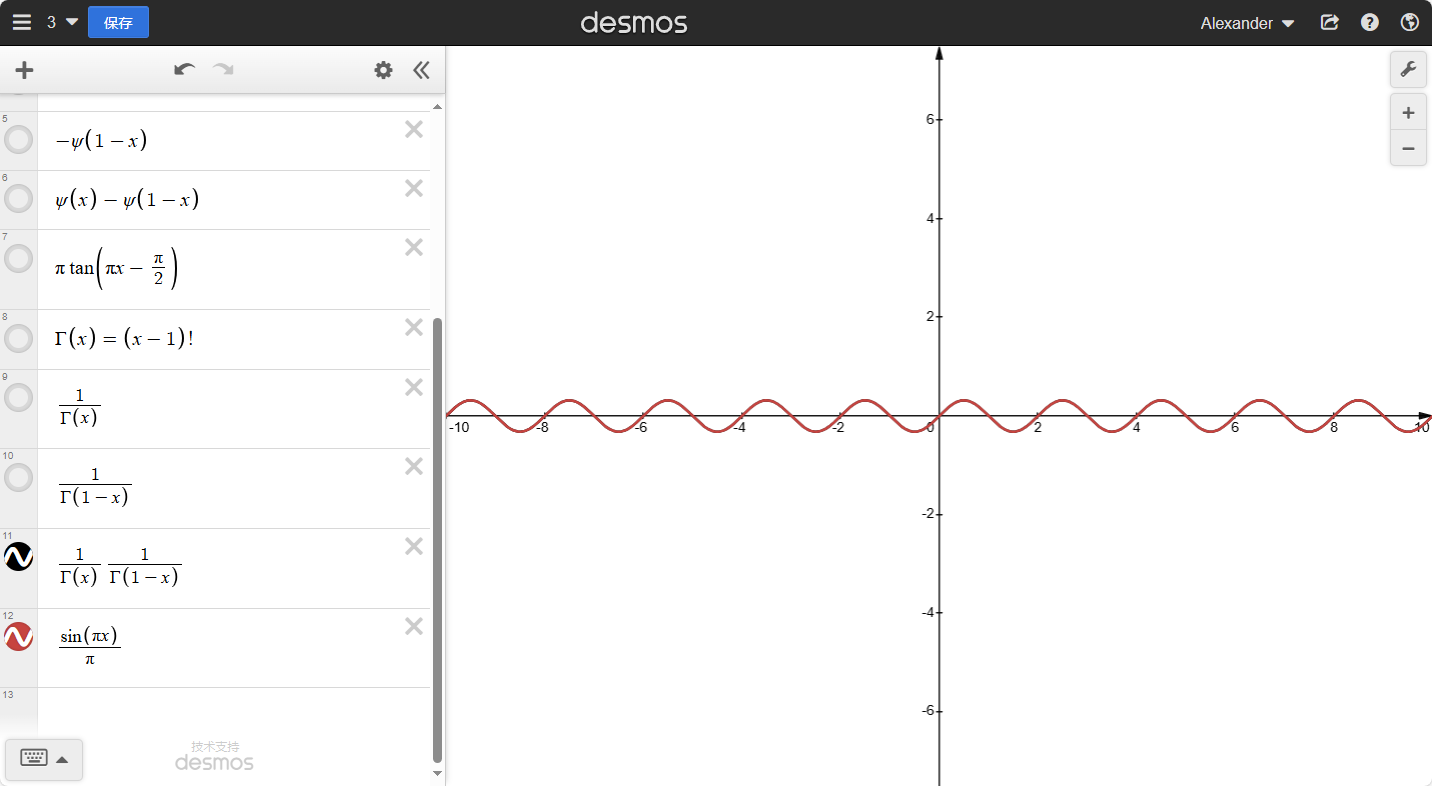
ψ(x)−ψ(1−x)=πtan(πx−2π)=−πcot(πx)
2.Γ(x)与sin(x)
这是Γ(x)的图像

仔细观察可以发现:x负半轴的每一个整数的位置都有一条垂直渐近线,如果取Γ(x)的倒数,那么每个整数的位置就变成了零点:

然后进行同样的操作:将函数翻过来:

最后再相乘:

结果就是:一个完美的正弦函数:πsin(πx)

我的天啊,这么神奇吗!!!随便糊弄一下,三角函数随机出现?
3.最后的真相
其实,答案是一种有趣的计算sinx的方式:正弦无穷乘积公式。(没错,还是欧拉······)
sinx=xk=1∏∞(1−π2k2x2)
我们先来证明一下这个东西,再说一下这个公式为什么有这样的联系。
Proof:
我们通过之前有的 n倍角公式,于是我们可以轻松得到:
sin(3x)=sinx(3−4sin2x)sin(5x)=sinx(5−20sin2x+16sin4x)
可以发现:sin(2n+1)x=sinx⋅P(sin2x)
其中P(x)指关于x的n次多项式。
先求出P(x)的常数项,由洛必达法则可以得到:
P(0)=x→0limsinxsin(2n+1)x=x→0limcosx(2n+1)cos(2n+1)x=2n+1
同时,由三角函数知识我们可以知道:sin(2n+1)x的根为2n+1kπ(k∈Z),所以sin22n+1kπ,k=1,2,...,n恰为P(x)的n个根。所以有:
P(x)=n→∞lim(2n+1)(1−sin22n+1πx)(1−sin22n+12πx)...(1−sin22n+1nπx)=n→∞lim(2n+1)k=1∏n(1−sin22n+1kπx)
把x替换成sinx,于是我们就可以得到:
n→∞limsinxsin(2n+1)x=n→∞lim(2n+1)k=1∏n(1−sin22n+1kπsin2x)
把x替换成2n+11x:
n→∞lim(2n+1)sin2n+11xsinx=n→∞limk=1∏n(1−sin22n+1kπsin22n+11x)n→∞lim(2n+1)sin2n+11x⋅∏k=1m(1−sin22n+1kπsin22n+11x)sinx=n→∞limk=m+1∏n(1−sin22n+1kπsin22n+11x)
为什么要这么干呢?因为要取极限:
左边取极限可以得到:x∏k=1m(1−k2π2x2)sinx,对于右边我们有:π2x<sinx<x,x∈(0,xπ),简单换元可以得到:
sin22n+11x<(2n+1)2x2sin22n+1kπ>(2n+1)24k2sin22n+1kπsin22n+11x<4k2x2
所以我们可以得到:
1>n→∞limk=m+1∏n(1−sin22n+1kπsin22n+11x)>k=m+1∏∞(1−4k2x2)
代入x∏k=1m(1−k2π2x2)sinx=limn→∞∏k=m+1n(1−sin22n+1kπsin22n+11x),可以得到:
1>x∏k=1m(1−k2π2x2)sinx>k=m+1∏∞(1−4k2x2)
再对m取极限,使得m→∞,可以得到左右两边极限都是1,所以根据极限夹逼准则,可得:
sinx=xk=1∏∞(1−k2π2x2)
Q.E.D.
这样,这个式子我们就算证明完成了。那么他和Γ(x)和ψ(x)有什么关系呢?
Γ(x+1)=N→∞limN1+x−1k=1∏N1+x−1+kkΓ(1−x)=N→∞limN1−x−1k=1∏N1−x−1+kkΓ(x)Γ(1−x)1=Γ(x+1)Γ(1−x)x=limN→∞(N1+x−1∏k=1N1+x−1+kk)limN→∞(N1−x−1∏k=1N1−x−1+kk)x
化简(消掉1,合并lim,再提出N?的那一项,合并∏)可以得到:
Γ(x+1)Γ(1−x)x=∏k=1∞x+kk×−x+kkx=x∏k=1∞k2−x2k21=xk=1∏∞k2k2−x2=xk=1∏∞(1−k2x2)
另一方面,sinx把x换成πx,可知:
πsin(πx)=xk=1∏∞(1−k2x2)
所以:
Γ(x)Γ(1−x)1=πsin(πx)
也就是:
Γ(x)Γ(1−x)=sin(πx)π
然后,我们两边取对数:
ln(Γ(x))+ln(Γ(1−x))=ln(π)−ln(sin(πx))
再取导数:
ψ(x)−ψ(1−x)=−πcot(πx)
Tip:
这里会发现我做了一堆违规的事情,比如取对数我没有考虑正负ln(sin(πx)),但是他们求导完是对的,原因是这里我们实际上并不是先去对数再取导数,我们做的叫取对数导数
参考资料:https://encyclopediaofmath.org/wiki/Logarithmic_derivative
对数导数本身的定义:
在数学中,特别是在微积分和复分析中,函数f的对数导数由以下公式定义:
ff′
完结,撒花。